题目内容
函数y=3sin（2x-
）+1的对称轴方程是 ．
| π |
| 4 |
考点：正弦函数的对称性
专题：三角函数的图像与性质
分析：对于函数y=3sin（2x-
）+1，令2x-
=kπ+
，k∈z，求得x的值，可得函数y=3sin（2x-
）+1的对称轴方程．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
解答：
解：对于函数y=3sin（2x-
）+1，令2x-
=kπ+
，k∈z，
求得x=
+
，k∈z，可得函数y=3sin（2x-
）+1的对称轴方程是x=
+
，k∈z，
故答案为：x=
+
，k∈z．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
求得x=
| kπ |
| 2 |
| 3π |
| 8 |
| π |
| 4 |
| kπ |
| 2 |
| 3π |
| 8 |
故答案为：x=
| kπ |
| 2 |
| 3π |
| 8 |
点评：本题主要考查正弦函数的图象的对称性，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
要得到一个奇函数，只需将函数f（x）=sin2x-
cos2x的图象（ ）
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
已知函数f（x）=
，若f（m）＜1，则m的取值范围是（ ）
|
| A、（-1，1） |
| B、（-∞，1） |
| C、（-1，0] |
| D、（0，1） |
如图是函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜
）的图象，则其解析式是（ ）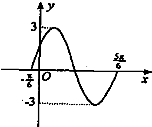
| π |
| 2 |
A、y=3sin(2x+
| ||
B、y=3sin(2x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(2x+
|
若命题p为真，命题q为假，则（ ）
| A、命题“p∧q”为真 |
| B、命题“p∨q”为真 |
| C、命题“￢p”为真 |
| D、命题“￢q”为假 |