题目内容
设a=sin(-1),b=cos(-1),c=tan(-1),则a,b,c的大小关系为 .
考点:三角函数线,不等式比较大小
专题:三角函数的求值
分析:由于-
<-1<-
,可得b=cos(-1)>0,0>a=sin(-1)>-
,c=tan(-1)<-
,即可得出.
| π |
| 3 |
| π |
| 4 |
| ||
| 2 |
| 3 |
解答:
解:∵-
<-1<-
,
∴b=cos(-1)>0,0>a=sin(-1)>-
,c=tan(-1)<-
,
∴c<a<b.
故答案为:c<a<b.
| π |
| 3 |
| π |
| 4 |
∴b=cos(-1)>0,0>a=sin(-1)>-
| ||
| 2 |
| 3 |
∴c<a<b.
故答案为:c<a<b.
点评:本题考查了三角函数的单调性,属于基础题.

练习册系列答案
相关题目
下面四个命题中的真命题是( )
| A、命题“?x≥2,均有x2-3x+2≥0”的否定是:“?x<2,使得x2-3x+2<0” |
| B、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| C、采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5、16、27、38、49的同学均被选出,则该班人数可能为60 |
| D、在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8 |
已知α∈(
,π),且sinα•cosα=-
,则sinα-cosα的值是( )
| 3π |
| 4 |
| ||
| 4 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
设变量x,y满足约束条件:
,则z=x-3y+4的最大值为( )
|
| A、8 | B、6 | C、4 | D、2 |
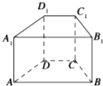 如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件
如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件