题目内容
将函数y=sin(x-
)的图象上所有点的纵坐标伸长到原来的2倍,再把所得的图象上所有点的横坐标向左平移
个单位长度后,得到函数f(x)的图象.
(1)求f(x)在[0,2π]上的单调递增区间;
(2)设函数g(x)=(1+sinx)f(x),求g(x)的值域.
| π |
| 3 |
| π |
| 3 |
(1)求f(x)在[0,2π]上的单调递增区间;
(2)设函数g(x)=(1+sinx)f(x),求g(x)的值域.
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:(1)变换后函数解析式为f(x)=2sinx,从而可得f(x)在[0,2π]上的单调递增区间是[0,
]∪[
,2π].
(2)化简得g(x)=2(sinx+
)2-
,从而可求g(x)的值域.
| π |
| 2 |
| 3π |
| 2 |
(2)化简得g(x)=2(sinx+
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:将函数y=sin(x-
)的图象上所有点的纵坐标伸长到原来的2倍,得到y=2sin(x-
)的图象;
再把所得的图象上所有点的横坐标向左平移
个单位长度后,得到函数f(x)=2sin[(x+
)-
]=2sinx的图象.
(1)∵f(x)=2sinx,正弦函数的单调递增区间是[2kπ-
,2kπ+
],k∈Z
∴f(x)在[0,2π]上的单调递增区间是[0,
]∪[
,2π].
(2)∵g(x)=(1+sinx)f(x)=(1+sinx)2sinx=2(sin2x+sinx)=2(sinx+
)2-
∵sinx∈[-1,1]
∴当sinx=1时,函数f(x)取到最大值为4,
当sinx=-
时,函数f(x)取到最小值为-
,
综上函数g(x)的值域是[-
,4].
| π |
| 3 |
| π |
| 3 |
再把所得的图象上所有点的横坐标向左平移
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(1)∵f(x)=2sinx,正弦函数的单调递增区间是[2kπ-
| π |
| 2 |
| π |
| 2 |
∴f(x)在[0,2π]上的单调递增区间是[0,
| π |
| 2 |
| 3π |
| 2 |
(2)∵g(x)=(1+sinx)f(x)=(1+sinx)2sinx=2(sin2x+sinx)=2(sinx+
| 1 |
| 2 |
| 1 |
| 2 |
∵sinx∈[-1,1]
∴当sinx=1时,函数f(x)取到最大值为4,
当sinx=-
| 1 |
| 2 |
| 1 |
| 2 |
综上函数g(x)的值域是[-
| 1 |
| 2 |
点评:本题主要考察了函数y=Asin(ωx+φ)的图象变换,三角函数的图象与性质,函数值域的解法,属于基本知识的考查.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
函数y=
+
( )
| 3-x2 |
| 9 |
| |x|+1 |
| A、只是偶函数 |
| B、只是奇函数 |
| C、既是偶函数,又是奇函数 |
| D、是非奇非偶函数 |
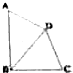 已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.
已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.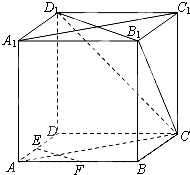 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.