题目内容
直线x-y-2=0关于直线x-y-1=0对称的直线方程是 .
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:求出两条平行线之间的距离,然后设出直线方程,利用平行线之间的距离相等求解即可.
解答:
解:直线x-y-2=0与直线x-y-1=0平行,所以平行线之间的距离为:
=
.
所求直线方程设为:x-y+b=0,
则:
=
,解得b=0或b=2(舍去).
所求直线方程为:x-y=0.
故答案为:x-y=0.
| |-2+1| | ||
|
| ||
| 2 |
所求直线方程设为:x-y+b=0,
则:
| |b+1| | ||
|
| ||
| 2 |
所求直线方程为:x-y=0.
故答案为:x-y=0.
点评:本题考查对称直线方程的求法,平行线之间的距离的求法,基本知识的考查.

练习册系列答案
相关题目
已知tanθ=2,则
=( )
sin(
| ||
sin(
|
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、
|
与角
终边相同的角是( )
| 11π |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若
=(-2,1,4),
=(3,2,-1)分别是直线l1,l2的方向向量,则( )
| a |
| b |
| A、l1∥l2 |
| B、l1⊥l2 |
| C、l1与l2相交 |
| D、l1与l2相交或异面 |
侧棱两两垂直的三棱锥V-ABC中,VA=a,VB=b,VC=c,则其外接球的表面积为( )
A、
| ||
B、
| ||
| C、π(a2+b2+c2) | ||
D、
|
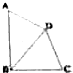 已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.
已知在四边形ABCD中,∠ABC=90°,BD平分∠ABC,∠ADC=135°,BC=8,AB=9,求CD的长.