Question

4．方程x²-cosx=0的解可视为函数y=cosx的图象与函数y=x²的图象交点的横坐标，则方程${x^2}-4xsin\frac{πx}{2}+1=0$实数解的个数为4．

Answer 1

分析 将方程变形得sin$\frac{πx}{2}$=$\frac{x}{4}+\frac{1}{4x}$（x≠0），分别作出y=sin$\frac{πx}{2}$和y=$\frac{1}{4}$（x+$\frac{1}{x}$）的函数图象，根据交点个数进行判断．

解答 解：∵${x^2}-4xsin\frac{πx}{2}+1=0$，∴sin$\frac{πx}{2}$=$\frac{x}{4}+\frac{1}{4x}$（x≠0），
令f（x）=$\frac{x}{4}+\frac{1}{4x}$=$\frac{1}{4}$（x+$\frac{1}{x}$），
则f（x）在（0，1）上单调递减，在（1，+∞）上单调递增，
做出y=sin$\frac{πx}{2}$和y=f（x）在（0，+∞）上函数图象如图所示：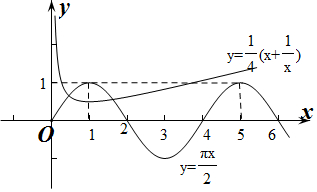

由图象可知y=sin$\frac{πx}{2}$和y=f（x）在（0，+∞）上有2个交点，
又y=sin$\frac{πx}{2}$和y=f（x）都是奇函数，
∴y=sin$\frac{πx}{2}$和y=f（x）在（-∞，0）上有2个交点，
∴方程${x^2}-4xsin\frac{πx}{2}+1=0$有4个解，
故答案为：4．

点评 本题考查了方程的根与函数图象的关系，属于中档题．