题目内容
14.已知公差不为零的等差数列{an}中,a1=1,且a1,a2,a5成等比数列(1)求数列{an}的通项公式;
(2)若bn=$\frac{1}{{a}_{n}{•a}_{n+1}}$,求数列{bn}的前n项和Tn.
分析 (1)设公差d不为零的等差数列{an},运用等比数列中项的性质和等差数列的通项公式,解方程可得d=2,进而得到所求通项公式;
(2)求得bn=$\frac{1}{{a}_{n}{•a}_{n+1}}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,化简计算即可得到所求和.
解答 解:(1)设公差d不为零的等差数列{an},
a1=1,且a1,a2,a5成等比数列,
可得a22=a1a5,
即为(1+d)2=1×(1+4d),
解得d=2,
则数列{an}的通项公式为an=a1+(n-1)d=1+2(n-1)=2n-1(n为正整数);
(2)bn=$\frac{1}{{a}_{n}{•a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
即有前n项和Tn=b1+b2+…+bn
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$(n为正整数).
点评 本题考查数列的通项公式的求法,注意运用等比数列中项的性质和等差数列的通项公式,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
5.依法纳税是每个公民应尽的义务,规定:公民全月工资、薪金所得不超过3500元的,免征个人所得税;超过3500元部分为全月应纳税所得额,此项税款按如表分段累计计算:
(1)若应纳税额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式;
(2)某人一月份应交纳此项税款303元,那么他当月的工资、薪金所得是多少?
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过1500元部分 | 3% |
| 2 | 超过1500元至4500元部分 | 10% |
| 3 | 超过4500元至9000元部分 | 20% |
(2)某人一月份应交纳此项税款303元,那么他当月的工资、薪金所得是多少?
2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m⊥α,m∥n,n∥β,则 α⊥β | B. | 若α∥β,m?α,n?β,则 m∥n | ||
| C. | 若m⊥n,m?α,n?β,则α⊥β | D. | 若α⊥β,m?α,n?β,则m⊥n |
19.如图所示,程序框图输出的结果是( )


| A. | 55 | B. | 89 | C. | 144 | D. | 233 |
6.三棱柱ABC-A1B1C1的侧棱垂直于底面,且AB⊥BC,AB=BC=AA1=2,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为( )
| A. | 48π | B. | 32π | C. | 12π | D. | 8π |
3.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”.今共有粮38石,按甲、乙、丙的顺序进行“衰分”,已知甲分得18石,则“衰分比”为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
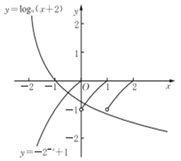 已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).
已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).