题目内容
8.设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A、B,则弦AB的垂直平分线的方程是( )| A. | 3x-2y-3=0 | B. | 3x-2y+3=0 | C. | 2x-3y-3=0 | D. | 2x-3y+3=0 |
分析 联立直线与圆的解析式得到交点A和B的坐标,然后利用中点坐标公式求出中点坐标,根据两直线垂直斜率乘积等于-1,由直线AB的斜率得到中垂线的斜率,即可得到中垂线的解析式.
解答 解:联立得:$\left\{\begin{array}{l}{2x+3y+1=0}\\{{x}^{2}{+y}^{2}-2x-3=0}\end{array}\right.$,
解得:13x2-14x-26=0,同理解得13y2+18y-7=0
因为点A和点B的中点M的坐标为(x=$\frac{{x}_{1}{+x}_{2}}{2}$,y=$\frac{{y}_{1}{+y}_{2}}{2}$),
利用根与系数的关系可得:M($\frac{7}{13}$,-$\frac{9}{13}$);
又因为直线AB:2x+3y+1=0的斜率为-$\frac{2}{3}$,
根据两直线垂直斜率乘积等于-1可知垂直平分线的斜率为$\frac{3}{2}$;
所以弦AB的垂直平分线方程为y+$\frac{9}{13}$=$\frac{3}{2}$(x-$\frac{7}{13}$),化简得3x-2y-3=0,
故选:A.
点评 考查学生掌握两直线垂直时的斜率乘积为-1,会求线段中点的坐标,根据条件能写出直线的一般方程,以及掌握直线与圆的方程的综合应用.

练习册系列答案
相关题目
19.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
16.A、B、C、D四名学生按任意次序站成一排,则A或B站在边上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{2}$ |
3.将4名同学录取到3所大学,则每所大学至少录取一名的概率为( )
| A. | $\frac{4}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
13.集合M={x|0<x<3,且x∈N}的子集个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
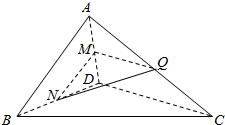 如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.
如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.