题目内容
20.一个样本由a,3,5,b构成,且a,b是方程x2-8x+5=0的两根,则这个样本的方差为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先求出a,b的值,求出这个样本的平均数,代入方差公式,求出方差的值即可.
解答 解:已知方程x2-8x+5=0,解方程得x1=4+$\sqrt{11}$,x2=4-$\sqrt{11}$;
∵a、b是方程x2-8x+5=0的两个根,
∴此样本是4+$\sqrt{11}$,4-$\sqrt{11}$,3,5,
平均数是:$\frac{1}{4}$(4+$\sqrt{11}$+4-$\sqrt{11}$+3+5)=4,
故方差是:$\frac{1}{4}$[${(4+\sqrt{11}-4)}^{2}$+${(4-\sqrt{11}-4)}^{2}$+(3-4)2+(5-4)2]=6,
故选:D.
点评 本题考察了解方程问题,考察求样本的平均数和方差问题,是一道基础题.

练习册系列答案
相关题目
8.设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A、B,则弦AB的垂直平分线的方程是( )
| A. | 3x-2y-3=0 | B. | 3x-2y+3=0 | C. | 2x-3y-3=0 | D. | 2x-3y+3=0 |
15.函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值之和为3,则a=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
12.已知集合U={1,2,3,4,5,6,7},集合A={2,4,5},则∁UA=( )
| A. | ∅ | B. | {1,3,5} | C. | {1,3,6,7} | D. | {1,3,5,7} |
10.在三角形ABC中,内角A,B,C所对的边分别为a,b,c,若acosA=bsinB,则sinAcosA+cos2B等于( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
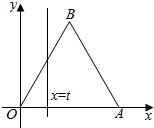 如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.
如图,△OAB是边长为2的正三角形,当一条垂直于底边OA(垂足不与O,A重合)的直线x=t从左至右移动时,直线l把三角形分成两部分,记直线l左边部分的面积y.