题目内容

18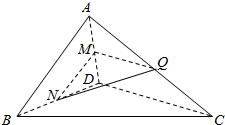．如图，在四面体ABCD中，AB⊥CD，AB⊥AD．M，N，Q分别为棱AD，BD，AC的中点．
（1）求证：CD∥平面MNQ；
（2）求证：平面MNQ⊥平面ACD．

分析 （1）利用M，Q分别为棱AD，AC的中点，证明MQ∥CD，即可证明CD∥平面MNQ；
（2）证明MN⊥平面ACD，即可证明平面MNQ⊥平面ACD．

解答 证明：（1）因为M，Q分别为棱AD，AC的中点，
所以MQ∥CD，…（3分）
又CD?平面MNQ，MQ?平面MNQ，
故CD∥平面MNQ．     …（7分）
（2）因为M，N分别为棱AD，BD的中点，所以MN∥AB，
又AB⊥CD，AB⊥AD，故MN⊥AD，MN⊥CD．  …（9分）
因为AD∩CD=D，AD，CD?平面ACD，所以MN⊥平面ACD
又MN?平面MNQ，所以平面MNQ⊥平面ACD． …（14分）

点评 本题考查线面平行，平面与平面垂直，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
8．“a+b是偶数”是“a、b都是偶数”的（　　）
A．充分不必要条件B．充要条件
C．必要不充分条件D．非充分非必要条件
9．某高三毕业班甲、乙两名同学在连续的8次数学周练中，统计解答题失分的茎叶图如下：
（1）比较这两名同学8次周练解答题失分的均值和方差的大小，并判断哪位同学做解答题相对稳定些；
（2）以上述数据统计甲、乙两名同学失分超过15分的频率作为频率，假设甲、乙两名同学在同一次周练中失分多少互不影响，预测在接下来的2次周练中，甲、乙两名同学失分均超过15分的次数X的分布列和均值．
6．已知函数$f（x）=\frac{2}{x+3}$．
（1）用定义证明：f（x）在（-3，+∞）上是减函数；
（2）求f（x）在[-1，2]上的最大值．
13．一个盒子里装有6张卡片，其中红色卡片4张，编号分别为3，6，8，9；蓝色卡片2张，编号分别为6，8，从盒子中任取3张卡片（假设取到任何一张卡片的可能性相同）．
（Ⅰ）求取出的3张卡片中，含有编号为6的卡片的概率；
（Ⅱ）记X为取到的卡片中红色卡片的张数，求X的分布列和数学期望．
3．“x=0”是“x=0”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分又不必要条件
10．已知函数f（x）=x3-ax2-bx+c有两个极值点x1，x2，若x1＜x2=f（x2），则f（x）=x1的解的个数为（　　）
A．0B．1C．2D．3
7．如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{2016}$的值的一个程序框图，则判断框内应填入的条件是（　　）
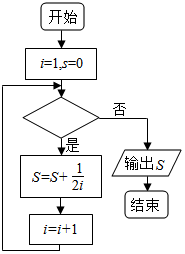
A．i≤1007B．i≤1008C．i＞1008D．i＞1007
8．设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A、B，则弦AB的垂直平分线的方程是（　　）
A．3x-2y-3=0B．3x-2y+3=0C．2x-3y-3=0D．2x-3y+3=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网