题目内容
抛物线y2=8x的焦点到双曲线x2-
=1的渐近线的距离是( )
| y2 |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先确定抛物线的焦点位置,进而可确定抛物线的焦点坐标,再由题中条件求出双曲线的渐近线方程,再代入点到直线的距离公式即可求出结论.
解答:
解:抛物线y2=8x的焦点在x轴上,且p=4,
∴抛物线y2=8x的焦点坐标为(2,0),
由题得:双曲线x2-
=1的渐近线方程为x±
y=0,
∴F到其渐近线的距离d=
=
.
故选:B.
∴抛物线y2=8x的焦点坐标为(2,0),
由题得:双曲线x2-
| y2 |
| 3 |
| ||
| 3 |
∴F到其渐近线的距离d=
| 2 | ||||
|
| 3 |
故选:B.
点评:本题考查抛物线的性质,考查双曲线的基本性质,解题的关键是定型定位,属于基础题.

练习册系列答案
相关题目
在(1-x3)(1+x)10的展开中,x5的系数是( )
| A、207 | B、297 |
| C、-297 | D、-252 |
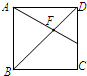 如图,正方形ABCD的边长为3,E为DC的中点,AE与BD相交于F,则
如图,正方形ABCD的边长为3,E为DC的中点,AE与BD相交于F,则| FD |
| DE |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
计算机中常用的十六进制是逢16进1的记数制,采用数字0-9和字母A-F共16个记数符号;这些符号与十进制的数的对应关系如下表:
例如,用十六进制表示:E+D=1B,则A×E=( )
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A、6E | B、8C | C、5F | D、82 |
如图,可作为函数y=f(x)的图象是( )
A、 |
B、 |
C、 |
D、 |
函数y=
在[2,3]上的最小值为( )
| 1 |
| x |
| A、2 | ||
B、
| ||
C、
| ||
D、-
|
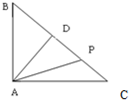 如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则
如图,已知△ABC中,AB=3,AC=4,BC=5,AD⊥BC于D点,点P为BC边所在直线上的一个动点,则| AP |
| AD |
| A、最大值为9 | ||
B、为定值
| ||
| C、最小值为3 | ||
| D、与P的位置有关 |
以下关于几何体的三视图的讨论中,正确的是( )
| A、球的三视图总是三个全等的圆 |
| B、正方体的三视图总是三个全等的正方形 |
| C、水平放置的正四面体的三视图都是正三角形 |
| D、水平放置的圆台的俯视图是一个圆 |
空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是( )
| A、垂直且相交 |
| B、相交但不一定垂直 |
| C、垂直但不相交 |
| D、不垂直也不相交 |