题目内容
对于直线ax+y-a=0（a≠0），以下说法正确的是（ ）
| A、恒过定点，且斜率和纵截距相等 |
| B、恒过定点，且横截距恒为定值 |
| C、恒过定点，且与y轴平行的直线 |
| D、恒过定点，且与x轴平行的直线 |
考点：恒过定点的直线
专题：直线与圆
分析：对于直线ax+y-a=0（a≠0），化为a（x-1）+y=0，令
，可得直线恒过定点（1，0），直线方程可化为：y=-ax+a，横纵截距分别为1，a为定值．
|
解答：
解：对于直线ax+y-a=0（a≠0），化为a（x-1）+y=0，
令
，解得x=1，y=0．
∴直线恒过定点（1，0），
直线方程可化为：y=-ax+a，横纵截距分别为1，a为定值．
故选：B．
令
|
∴直线恒过定点（1，0），
直线方程可化为：y=-ax+a，横纵截距分别为1，a为定值．
故选：B．
点评：本题考查了“直线系”、截距的意义，属于基础题．
练习册系列答案
相关题目
已知a＞1，在约束条件
下，目标函数z=x+ay的最大值小于2，则a的取值范围是（ ）
|
| A、（1，3） | ||
| B、（3，+∞） | ||
C、（
| ||
D、（1，
|
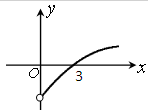已知f（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，当x＞0时，y=f（x）的图象如图所示，解不等式xf（x）＜0．