题目内容
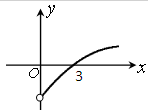已知f（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，当x＞0时，y=f（x）的图象如图所示，解不等式xf（x）＜0．考点：奇偶性与单调性的综合
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：根据图象可得，当x＞0时，f（x）递增，且f（3）=0，再由偶函数的图象关于y轴对称，可得x＜0时，f（x）递减，且f（-3）=0，不等式xf（x）＜0，即为
或
，分别解出它们，再求并集即可．
|
|
解答：
解：f（x）是定义在（-∞，0）∪（0，+∞）上的偶函数，
则由图象可得，当x＞0时，f（x）递增，且f（3）=0，
由于f（-x）=f（x），即有f（-3）=0，
再由偶函数的图象关于y轴对称，可得x＜0时，f（x）递减．
则不等式xf（x）＜0，即为
或
，
即有
或
，
即有
或
，
解得，0＜x＜3或x＜-3．
则解集为（0，3）∪（-∞，-3）．
则由图象可得，当x＞0时，f（x）递增，且f（3）=0，
由于f（-x）=f（x），即有f（-3）=0，
再由偶函数的图象关于y轴对称，可得x＜0时，f（x）递减．
则不等式xf（x）＜0，即为
|
|
即有
|
|
即有
|
|
解得，0＜x＜3或x＜-3．
则解集为（0，3）∪（-∞，-3）．
点评：本题考查函数的奇偶性和单调性的运用：解不等式，注意讨论的方法，考查运算能力，属于中档题．
练习册系列答案
相关题目
对于直线ax+y-a=0（a≠0），以下说法正确的是（ ）
| A、恒过定点，且斜率和纵截距相等 |
| B、恒过定点，且横截距恒为定值 |
| C、恒过定点，且与y轴平行的直线 |
| D、恒过定点，且与x轴平行的直线 |