题目内容
10．
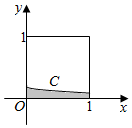在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C为正态分布N（-2，1）的密度曲线）的点的个数的估计值为（ ）[附：若X～N（μ，σ2），则P（μ-σ＜X＜μ+σ）=0.6826，
P（μ-2σ＜X＜μ+2σ）=0.9544，
P（μ-3σ＜X＜μ+3σ）=0.9974]．
| A． | 430 | B． | 215 | C． | 2718 | D． | 1359 |
分析 由正态分布曲线的特点，数形结合可得落入阴影部分的概率，乘以10000可得答案．
解答 解：∵X～N（-2，1），∴阴影部分的面积S=P（0≤X≤1）
=$\frac{1}{2}$[P（-5≤x≤1）-P（-4≤x≤0）]=$\frac{1}{2}$（0.9974-0.9544）=0.0215，
∴落入阴影部分的点的个数的估计值为10000×0.0215=215
故选：B．
点评 本题考查正态分布曲线的特点，数形结合是解决问题的关键，属基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
1．下列命题中错误的是（ ）
| A． | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| B． | 圆锥的轴截面是所在过顶点的截面中面积最大的一个 | |
| C． | 圆台的所有平行于底面的截面都是圆面 | |
| D． | 圆锥所有的轴截面是全等的等腰三角形 |
5．已知a+2b=1且b＞1，则$\frac{1}{a}$+$\frac{a}{b}$的取值范围（ ）
| A． | （-2，1-2$\sqrt{2}$] | B． | （-∞，1-2$\sqrt{2}$] | C． | [1+2$\sqrt{2}$，+∞） | D． | [1+2$\sqrt{2}$，4] |
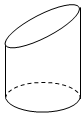用一个不平行于底面的平面截一个底面直径为6cm的圆柱，得到如图几何体，若截面椭圆的长轴长为10cm，这个几何体最短的母线长为6cm，则此几何体的体积为90πcm3．