题目内容
12.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,图象的一个对称中心为($\frac{π}{4}$,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移$\frac{π}{2}$个单位长度后得到函数g(x)的图象.(1)求函数f(x)与g(x)的解析式;
(2)求证:存在x0∈($\frac{π}{6}$,$\frac{π}{4}$),使得f(x0),g(x0),f(x0)•g(x0)能按照某种顺序成等差数列.
分析 (1)由周期公式可得ω,ω>0,再由对称中心可得φ值,可得f(x)解析式,由函数图象变换和诱导公式化简可得;
(2)当x∈($\frac{π}{6}$,$\frac{π}{4}$)时sinx>cos2x>sinx•cos2x,问题转化为方程2cos2x=sinx+sinx•cos2x在($\frac{π}{6}$,$\frac{π}{4}$)内是否有解,由函数零点的存在性定理可得.
解答 解:(1)∵函数f(x)=sin(ωx+φ)的周期为π,ω>0,∴$ω=\frac{2π}{T}=2$,
又曲线y=f(x)的一个对称中心为($\frac{π}{4}$,0),φ∈(0,π),
∴sin(2×$\frac{π}{4}$+φ)=0,可得$φ=\frac{π}{2}$,∴f(x)=cos2x,
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,
再将y=cosx的图象向右平移$\frac{π}{2}$个单位长度后得到函数g(x)=cos(x-$\frac{π}{2}$)的图象,
由诱导公式化简可得g(x)=sinx;
(2)当x∈($\frac{π}{6}$,$\frac{π}{4}$)时,$\frac{1}{2}<sinx<\frac{{\sqrt{2}}}{2}$,$0<cos2x<\frac{1}{2}$,
∴sinx>cos2x>sinx•cos2x,
问题转化为方程2cos2x=sinx+sinx•cos2x在($\frac{π}{6}$,$\frac{π}{4}$)内是否有解.
设G(x)=sinx+sinx•cos2x-2cos2x,x∈($\frac{π}{6}$,$\frac{π}{4}$),
∵$G(\frac{π}{6})=-\frac{1}{4}<0$,$G(\frac{π}{4})=\frac{{\sqrt{2}}}{2}>0$,且函数G(x)的图象连续不断,
∴函数G(x)在($\frac{π}{6}$,$\frac{π}{4}$)内存在零点x0,
即存在x0∈($\frac{π}{6}$,$\frac{π}{4}$),使得f(x0),g(x0),f(x0)•g(x0)能按照某种顺序成等差数列.
点评 本题考查三角函数图象变换,问题转化为方程2cos2x=sinx+sinx•cos2x在($\frac{π}{6}$,$\frac{π}{4}$)内是否有解是解决问题的关键,属中档题.

| A. | 向左平移1个单位长度 | B. | 向右平移1个单位长度 | ||
| C. | 向左平移$\frac{1}{3}$个单位长度 | D. | 向右平移$\frac{1}{3}$个单位长度 |
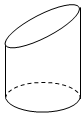 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.