题目内容
18.已知数列{an}中,首项a1=1,分别求出满足下列条件数列的通项公式.(1)an+1=an+3n2+3n+1(n∈N*)
(2)nan=a1+2a2+3a3+…+(n-1)an-1(n≥2,n∈N*)
分析 (1)由an+1=an+3n2+3n+1可得a2-a1=3×12+3×1+1,a3-a2=3×22+3×2+1,…,从而利用累加法求解;
(2)化简nan=a1+2a2+3a3+…+(n-1)an-1可得(n+1)an+1=2nan,从而可得数列{nan}从第2项起成以1为首项,2为公比的等比数列,从而解得.
解答 解:(1)∵an+1=an+3n2+3n+1,
∴a2-a1=3×12+3×1+1,
a3-a2=3×22+3×2+1,
…,
an-an-1=3×(n-1)2+3×(n-1)+1,
累加可得,
an-a1=(3×12+3×1+1)+(3×22+3×2+1)+…+(3×(n-1)2+3×(n-1)+1),
an-a1=3$\frac{(n-1)n(2n-1)}{6}$+3$\frac{1+n-1}{2}$•(n-1)+n-1,
=(n-1)(n2+n+1),
故an=(n-1)(n2+n+1)+1;
(2)∵nan=a1+2a2+3a3+…+(n-1)an-1,
∴(n+1)an+1=a1+2a2+3a3+…+(n-1)an-1+nan,
∴(n+1)an+1-nan=nan,
∴(n+1)an+1=2nan,
又∵1•a1=1,2a2=a1=1,
∴数列{nan}从第2项起成以1为首项,2为公比的等比数列,
∴nan=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-2},n≥2}\end{array}\right.$,
故an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{{2}^{n-2}}{n},n≥2}\end{array}\right.$.
点评 本题考查了等差数列与等比数列的性质及累加法与作差法的应用.

 中考解读考点精练系列答案
中考解读考点精练系列答案
| A. | 8 | B. | 21 | C. | 34 | D. | 55 |
| A. | $\frac{4}{27}$ | B. | $\frac{3}{25}$ | C. | $\frac{5}{28}$ | D. | $\frac{2}{15}$ |
| A. | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| B. | 圆锥的轴截面是所在过顶点的截面中面积最大的一个 | |
| C. | 圆台的所有平行于底面的截面都是圆面 | |
| D. | 圆锥所有的轴截面是全等的等腰三角形 |
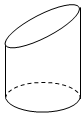 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.