题目内容
17.已知随机变量X服从正态分布N(4,σ2),且P(2<X≤6)=0.98,则P(X<2)=0.01.分析 随机变量X服从正态分布N(4,σ2),根据对称性,由P(2<X≤4)的概率可求出P(X<2).
解答 解:∵随机变量X服从正态分布N(4,σ2),且P(2<X≤6)=0.98,
∴P(2<X≤4)=$\frac{1}{2}$P(2<X≤6)=0.49,
∴P(X<2)=0.5-P(2<X≤4)=0.5-0.49=0.01.
故答案为:0.01.
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义,注意根据正态曲线的对称性解决问题.

练习册系列答案
相关题目
8.已知随机变量ξ服从正态分布N(3,σ2),P(ξ≤4)=0.842,则P(ξ≤2)=( )
| A. | 0.842 | B. | 0.158 | C. | 0.421 | D. | 0.316 |
5.已知a+2b=1且b>1,则$\frac{1}{a}$+$\frac{a}{b}$的取值范围( )
| A. | (-2,1-2$\sqrt{2}$] | B. | (-∞,1-2$\sqrt{2}$] | C. | [1+2$\sqrt{2}$,+∞) | D. | [1+2$\sqrt{2}$,4] |
9.已知i2=-1,复数z=$\frac{1-i}{1+i}$,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
6.在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}$•$\overrightarrow{AC}$≥1的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
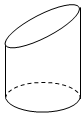 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.