题目内容
已知a，b，c是△ABC中∠A，∠B，∠C所对的边，如果a=
，b=
，∠B=60°，那么∠A等于（ ）
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、60° |
考点：正弦定理
专题：解三角形
分析：由条件利用正弦定理求得sinA=
，再由a＜b，可得A＜B，从而确定A的值．
| ||
| 2 |
解答：
解：△ABC中，由于a=
，b=
，∠B=60°，故由正弦定理可得
=
，
求得sinA=
．由于a＜b，∴A＜B，∴A=45°，
故选：B．
| 2 |
| 3 |
| ||
| sinA |
| ||
| sin60° |
求得sinA=
| ||
| 2 |
故选：B．
点评：本题主要考查正弦定理的应用，大边对大角，属于基础题．
练习册系列答案
相关题目
已知角α的终边经过点P（-1，3），则sinα-2cosα=（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
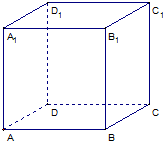如图，在正方体ABCD-A1B1C1D1中，E，F分别为AB、AD的中点，