题目内容
9.已知1+i是关于x的方程2x2+px+q=0(p,q∈R)的一个根,则|p+qi|( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
分析 1+i是关于x的方程2x2+px+q=0(p,q∈R)的一个根,则1-i也是关于x的方程2x2+px+q=0(p,q∈R)的一个根,利用根与系数的关系、模的计算公式即可得出.
解答 解:∵1+i是关于x的方程2x2+px+q=0(p,q∈R)的一个根,则1-i也是关于x的方程2x2+px+q=0(p,q∈R)的一个根,
∴1+i+1-i=-$\frac{p}{2}$,(1+i)(1-i)=$\frac{q}{2}$,
解得p=-4,q=4.
则|p+qi|=|-4+4i|=$\sqrt{(-4)^{2}+{4}^{2}}$=4$\sqrt{2}$.
故选:D.
点评 本题考查了实系数一元二次方程的根与系数的关系、模的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
20.已知$f(x)=\left\{\begin{array}{l}(3-a)x-a,x<1\\{log_a}x,x≥1\end{array}\right.$是(-∞,+∞)上的增函数,那么实数a的取值范围是( )
| A. | (1,+∞) | B. | (1,3) | C. | (0,1)∪(1,3) | D. | $[\frac{3}{2},3)$ |
17.已知函数$f(x)={x^{\frac{1}{2}}}$,则( )
| A. | ?x0∈R,使得f(x)<0 | |
| B. | ?x∈[0,+∞),f(x)≥0 | |
| C. | ?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$ | |
| D. | ?x1∈[0,+∞),?x2∈[0,+∞)使得f(x1)>f(x2) |
14.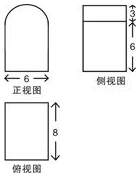 已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
 已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )| A. | 36π+288 | B. | 36π+216 | C. | 33π+288 | D. | 33π+216 |