题目内容
20．已知$f（x）=\left\{\begin{array}{l}（3-a）x-a，x＜1\\{log_a}x，x≥1\end{array}\right.$是（-∞，+∞）上的增函数，那么实数a的取值范围是（ ）| A． | （1，+∞） | B． | （1，3） | C． | （0，1）∪（1，3） | D． | $[\frac{3}{2}，3）$ |
分析 根据一次函数以及对数函数的性质结合函数的单调性求出a的范围即可．
解答 解：∵$f（x）=\left\{\begin{array}{l}（3-a）x-a，x＜1\\{log_a}x，x≥1\end{array}\right.$是（-∞，+∞）上的增函数，
∴$\left\{\begin{array}{l}{3-a＞0}\\{a＞1}\\{3-a-a≤0}\end{array}\right.$，解得：$\frac{3}{2}$≤a＜3，
故选：D．
点评 本题考查了函数的单调性问题，考查一次函数以及对数函数的性质，是一道基础题．
练习册系列答案
相关题目
10．下方茎叶图如图1，为高三某班50名学生的数学考试成绩，算法框图如图2中输入的ai为茎叶图中的学生成绩，则输出的m，n分别是（ ）
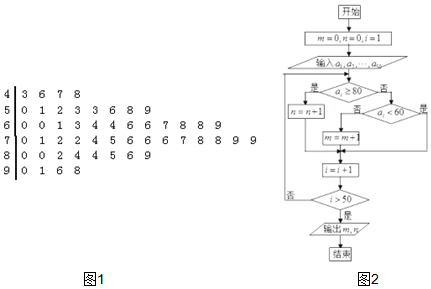
| A． | m=26，n=12 | B． | m=38，n=12 | C． | m=12，n=12 | D． | m=24，n=10 |
11．已知函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{3}}}x，x＞0\\{2^x}，x≤0\end{array}\right.$，若$f（a）＞\frac{1}{2}$，则实数a的取值范围是（ ）
| A． | $（{0，\frac{{\sqrt{3}}}{3}}）$ | B． | （-1，0] | C． | $（{-1，\frac{{\sqrt{3}}}{3}}）$ | D． | $（{-1，0}）∪（{0，\frac{{\sqrt{3}}}{3}}）$ |
8．
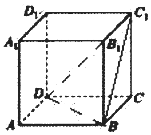在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）
在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
5．如图所示是用模拟方法估计圆周率π值的程序框图，m表示估计结果，则图中空白处应填入（ ）
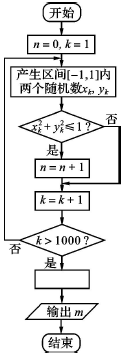
| A． | $m=\frac{n}{4000}$ | B． | $m=\frac{n}{1000}$ | C． | $m=\frac{n}{500}$ | D． | $m=\frac{n}{250}$ |
9．已知1+i是关于x的方程2x2+px+q=0（p，q∈R）的一个根，则|p+qi|（ ）
| A． | $\sqrt{2}$ | B． | $2\sqrt{2}$ | C． | $3\sqrt{2}$ | D． | $4\sqrt{2}$ |