题目内容
19.函数$f(x)=\left\{\begin{array}{l}{x^3}-3x,x≤0\\-2x+1,x>0\end{array}\right.$,则f(x)的最大值是( )| A. | 0 | B. | 2 | C. | 1 | D. | 3 |
分析 讨论当x>0时,运用一次函数的单调性,可得f(x)的范围;当x≤0时,求出f(x)的导数,单调区间和极大值,也为最大值,即可得到所求最大值.
解答 解:当x>0时,f(x)=1-2x递减,
可得f(x)<1;
当x≤0时,f(x)=x3-3x,
导数f′(x)=3x2-3=3(x-1)(x+1),
当-1<x<0时,f′(x)<0,f(x)递减;
当x<-1时,f′(x)>0,f(x)递增.
可得x=-1处f(x)取得极大值,且为最大值-1+3=2.
则f(x)的最大值为2.
故选:B.
点评 本题考查分段函数的运用:求最值,注意考虑各段的最值,以及导数的运用:求单调区间和极值、最值,考查分类讨论的思想方法,以及判断比较能力,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.已知1+i是关于x的方程2x2+px+q=0(p,q∈R)的一个根,则|p+qi|( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
10.$sin40°(tan10°-\sqrt{3})$=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
7.△ABC内一点O满足$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=0$,直线AO交BC于点D,则( )
| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
4.某三棱锥的三视图是三个边长相等的正方形及对角线,若该几何体的体积是$\frac{1}{3}$,则它的表面积是( )
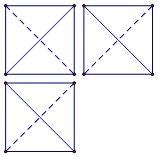

| A. | 1 | B. | 2 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
11.已知复数z=(t-1)+(t+1)i,t∈R,|z|的最小值是( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |