题目内容
函数y=loga（x-3）-1的图象恒过与a无关的定点 ．
考点：对数函数的单调性与特殊点
专题：函数的性质及应用
分析：令对数的真数x-3=1，求得 x和y的值，可得定点的坐标．
解答：
解：∵函数y=loga（x-3）-1的图象恒过与a无关的定点，
∴x-3=1，求得 x=4，y=-1，故定点的坐标为（4，-1），
故答案为：（4，-1）．
∴x-3=1，求得 x=4，y=-1，故定点的坐标为（4，-1），
故答案为：（4，-1）．
点评：本题主要考查对数函数的单调性和特殊点，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
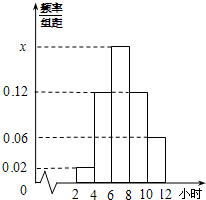某校为了解学生寒假期间的学习情况，从初中及高中各班共抽取了50名学生，对他们每天平均学习时间进行统计．请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题：
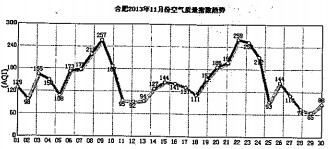合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图．