题目内容
 如图,在底面积边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面积边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.(1)若m=1,求异面直线AP与BD1所成的余弦值;
(2)是否存在实数m,使直线AP与平面AB1D1所成的正弦值是
| 1 |
| 3 |
考点:异面直线及其所成的角,直线与平面所成的角
专题:空间角
分析:(1)以点D为坐标原点,DA为x轴,DB为y轴,D1D为z轴,建立空间直角坐标系,分别求出向量
,
的坐标,利用向量的夹角公式求出夹角,从而求出异面直线AE与BD1所成角的余弦值.
(2)假设存在,得到直线AP与平面AB1D1的法向量夹角的余弦值的绝对值是
,找出法向量与向量AP,计算数量积解m.
| AP |
| BD1 |
(2)假设存在,得到直线AP与平面AB1D1的法向量夹角的余弦值的绝对值是
2
| ||
| 3 |
解答:
解:(1)如图所示,建立空间直角坐标系,
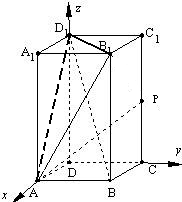
则A(1,0,0),P(0,1,1),B(1,1,0),D1(0,0,2)
∴
=(-1,1,1),
=(-1,-1,2)
∴
•
=2,又AP=
,BD1=
∴cos<
,
>=
=
=
,
∴异面直线AE与BD1所成角的余弦值等于
;
(2)假设存在实数m,使直线AP与平面AB1D1所成的正弦值是
,则直线AP与平面AB1D1的法向量夹角的余弦值的绝对值是
,
则A(1,0,0),P(0,1,m),B1(1,1,2),D1(0,0,2),
∴
=(-1,1,m),
=(0,1,2),
=(-1,-1,0),
设平面AB1D1的法向量为
=(x,y,z),则
,所以
,
令z=1,则一个法向量
=(2,-2,1),
|cos<
,
>|=|
|=|
|=
,解得m=0或m=
,满足m∈[0,2],
所以存在实数m=0或者m=
,使直线AP与平面AB1D1所成的正弦值是
.

则A(1,0,0),P(0,1,1),B(1,1,0),D1(0,0,2)
∴
| AP |
| BD1 |
∴
| AP |
| BD1 |
| 3 |
| 6 |
∴cos<
| AP |
| BD1 |
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
∴异面直线AE与BD1所成角的余弦值等于
| ||
| 3 |
(2)假设存在实数m,使直线AP与平面AB1D1所成的正弦值是
| 1 |
| 3 |
2
| ||
| 3 |
则A(1,0,0),P(0,1,m),B1(1,1,2),D1(0,0,2),
∴
| AP |
| AB1 |
| B1D1 |
设平面AB1D1的法向量为
| n |
|
|
令z=1,则一个法向量
| n |
|cos<
| AP |
| n |
| ||||
|
|
| -4+m | ||
3
|
2
| ||
| 3 |
| 8 |
| 7 |
所以存在实数m=0或者m=
| 8 |
| 7 |
| 1 |
| 3 |
点评:本题考查了四棱柱中异面直线所成的角和线面角,本题借助于空间向量的数量积解答,注意适当建立坐标系,正确找出所需向量的坐标.

练习册系列答案
相关题目
已知α,β∈[-
,
],且αsinα-βsinβ>0,则下列结论正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、α3>β3 |
| B、α+β>0 |
| C、|α|<|β| |
| D、|α|>|β| |
对于非空数集A,若实数M满足对任意的a∈A恒有a≤M,则M为A的上界;若A的所有上界中存在最小值,则称此最小值为A的上确界,那么下列函数的值域中具有上确界的是( )
A、y=
| ||||
B、y=(-
| ||||
C、y=
| ||||
| D、y=lnx |
若函数y1=2sinx(x∈[0,2π))在P处的切线平行于函数y2=2
(
+1)在Q处的切线,则直线PQ的斜率为( )
| x |
| x |
| 3 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
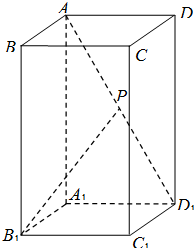 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).