题目内容
9.若函数f(x)=-x2-10x在(-∞,λ]上是增函数,则方程组$\left\{\begin{array}{l}({λ-1})x+4y=1\\ 3x+λy=2\end{array}\right.$的解的组数为1.分析 利用函数的单调性求出λ,然后求解方程组的解即可.
解答 解:函数f(x)=-x2-10x在(-∞,λ]上是增函数,
可得λ=-$\frac{10}{2}$=-5,则方程组$\left\{\begin{array}{l}({λ-1})x+4y=1\\ 3x+λy=2\end{array}\right.$,化为:$\left\{\begin{array}{l}{-6x+4y=1}\\{3x-6y=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{23}{12}}\\{y=-\frac{5}{8}}\end{array}\right.$,
方程组只有一组解.
故答案为:1.
点评 本题考查二次函数的性质的应用,方程组的求法,考查计算能力.

练习册系列答案
相关题目
20.下列四组函数中,表示同一个函数的是( )
| A. | f(x)=|x+1|,g(x)=$\left\{\begin{array}{l}{x+1(x≥-1)}\\{-1-x(x<-1)}\end{array}\right.$ | B. | f(x)=$\frac{{x}^{2}-1}{x+1}$,g(x)=x-1 | ||
| C. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | D. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ |
17.若点(1,-3)在圆(x-2)2+(y+1)2=m的内部,则实数m的取值范围是( )
| A. | 0<m<10 | B. | 0<m<5 | C. | m>5 | D. | m<5 |
14.若函数f(x)=xlnx-ax2有两个极值点,则实数a的取值范围是( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (1,2) | D. | (2,e) |
1.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤3}\\{x-y≥-1}\\{y≥1}\end{array}\right.$,则目标函数z=4x+2y的最大值为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2 |
19.设区间[q,p]的长度为p-q,其中p>q.现已知两个区间[4lnm,ln2m]与[lnm,4lnm-10]的长度相等,则ex+1+me-x的最小值为( )
| A. | 2e3 | B. | $2{e^{\frac{3}{2}}}$或2e3 | C. | $2{e^{\frac{3}{2}}}$ | D. | $2{e^{\frac{3}{2}}}$或2e2 |
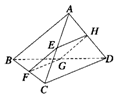 如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.
如图所示,四边形EFGH为空间四边形ABCD的一个截面,若CD∥面EFGH,求证:EH∥FG.