题目内容
 在椭圆中,过焦点且垂直于长轴的直线被椭圆截得的弦,叫做椭圆的通径.如图,已知椭圆
在椭圆中,过焦点且垂直于长轴的直线被椭圆截得的弦,叫做椭圆的通径.如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆的方程;
(2)过F2的动直线l交椭圆于A、B两点,
(ⅰ)问在x轴上是否存在定点C,使
| CA |
| CB |
(ⅱ)延长BF1交椭圆于点M,I1、I2分别为△F1BF2、△F1MF2的内心,证明四边形F1I2F2I1与△MF2B的面积的比值恒为定值,并求出这个定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=
,
=3,由此能求出椭圆的方程.
(2)(ⅰ)当直线BM的斜率不为0时,设BM:x=my+1,联立方程
得(3m2+4)y2+6my-9=0.由此能求出
•
=-
,直线BM的斜率为0时,
•
=-
也成立.所以在x轴上存在定点C(
,0),使
•
为常数.
(ⅱ)椭圆的方程为
+
=1,c=1,由已知条件推导出S△F1I1F2:S△F1BF2=1:3,S△F1I2F2:S△F1AF2=1:3.从而得到四边形F1I2F2I1与△AF2B的面积的比值为
.
| c |
| a |
| 1 |
| 2 |
| 2b2 |
| a |
(2)(ⅰ)当直线BM的斜率不为0时,设BM:x=my+1,联立方程
|
| CM |
| CB |
| 135 |
| 64 |
| CM |
| CB |
| 135 |
| 64 |
| 11 |
| 8 |
| CM |
| CB |
(ⅱ)椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 3 |
解答:
(1)解:由
=
,得:a=2c.又通径长为3,
由x=c代入椭圆方程得y2=
,
则
=3,解得a=2,b=
.
∴椭圆的方程为
+
=1.…(4分)
(2)(ⅰ)解:假设在x轴上存在定点C(n,0),使
•
为常数.
①当直线BM的斜率不为0时,设BM:x=my+1,
联立方程
得(3m2+4)y2+6my-9=0.
设B(x1,y1),M(x2,y2),
则△>0恒成立,y1+y2=-
,y1y2=-
,…(6分)
所以(x1-n)(x2-n)=(my1+1-n)(my2+1-n)
=m2y1y2+m(1-n)(y1+y2)+(1-n)2
=-
-
+(1-n)2
=
,
•
=(x1-n)(x2-n)+y1y2=
=n2-4-
.
因为
•
与m无关,则n=
时,
•
=(
)2-4=-
.
②直线BM的斜率为0时,
•
=-
也成立
故在x轴上存在定点C(
,0),使
•
为常数.…(10分)
(ⅱ)证明:椭圆的方程为
+
=1,c=1,
设△F1BF2的内切圆的半径为r,
则S△F1BF2=
(|BF1|+|BF2|+|F1F2|)•r=3r,S△F1I1F2=
•|F1F2|•r=r.
则S△F1I1F2:S△F1BF2=1:3,同理得,S△F1I2F2:S△F1AF2=1:3.
所以,p=SF1I2F2I1:S△AF2B=1:3
四边形F1I2F2I1与△AF2B的面积的比值为
.…(14分)
| c |
| a |
| 1 |
| 2 |
由x=c代入椭圆方程得y2=
| b4 |
| a2 |
则
| 2b2 |
| a |
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)(ⅰ)解:假设在x轴上存在定点C(n,0),使
| CM |
| CB |
①当直线BM的斜率不为0时,设BM:x=my+1,
联立方程
|
得(3m2+4)y2+6my-9=0.
设B(x1,y1),M(x2,y2),
则△>0恒成立,y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
所以(x1-n)(x2-n)=(my1+1-n)(my2+1-n)
=m2y1y2+m(1-n)(y1+y2)+(1-n)2
=-
| 9m2 |
| 3m2+4 |
| 6m2(1-n) |
| 3m2+4 |
=
| 3m2n2-12m2+4n2-8n+4 |
| 3m2+4 |
| CM |
| CB |
| 3m2n2-12m2+4n2-8n-5 |
| 3m2+4 |
| 8n-11 |
| 3m2+4 |
因为
| CM |
| CB |
| 11 |
| 8 |
| CM |
| CB |
| 11 |
| 8 |
| 135 |
| 64 |
②直线BM的斜率为0时,
| CM |
| CB |
| 135 |
| 64 |
故在x轴上存在定点C(
| 11 |
| 8 |
| CM |
| CB |
(ⅱ)证明:椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
设△F1BF2的内切圆的半径为r,
则S△F1BF2=
| 1 |
| 2 |
| 1 |
| 2 |
则S△F1I1F2:S△F1BF2=1:3,同理得,S△F1I2F2:S△F1AF2=1:3.
所以,p=SF1I2F2I1:S△AF2B=1:3
四边形F1I2F2I1与△AF2B的面积的比值为
| 1 |
| 3 |
点评:本题考查椭圆方程的求法,考查使得向量的数量积为常数的点的坐标是否存在的判断与求法,考查四边形与三角形的面积比恒定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知数列{an}的前n项和Sn=n2-5n+4,第k项满足5<ak<8,则k等于( )
| A、4 | B、5 | C、6 | D、7 |
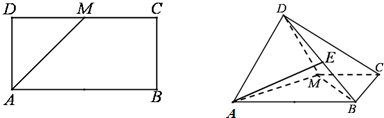 如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.