题目内容
已知数列{an}为a0,a1,a2,a3,…,an(n∈N),bn=
ai表示a0+a1+a2+a3+…+an,i∈N.
(1)若数列{an}为等比数列an=2n(n∈N),求
(biC
);
(2)若数列{an}为等差数列an=2n(n∈N),求
(biC
).
| n |
 |
| i=0 |
(1)若数列{an}为等比数列an=2n(n∈N),求
| n |
 |
| i=0 |
i n |
(2)若数列{an}为等差数列an=2n(n∈N),求
| n |
 |
| i=1 |
i n |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件得
(bi
)=(21-1)
+(22-1)
+(23-1)
+…+(2n+1-1)
,由此利用分组求和法能求出结果.
(2)由已知条件得
(bi
)=1•2•
+2•3•
+3•4•
+…+n(n+1)
,由此利用导数性质能求出结果.
| n |
 |
| i=0 |
| C | i n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
(2)由已知条件得
| n |
 |
| i=0 |
| C | i n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
解答:
解:(1)∵an=2n,bn=
ai,
∴bn=20+21+22+…+2n=2n+1-1,
∴
(bi
)=(21-1)
+(22-1)
+(23-1)
+…+(2n+1-1)
=21•
-1•
+22•
-1•
+23•
-1•
+…+2n+1•
-1•
=2(
+21•
+22•
+…+2n•
)-(
+
+
+…+
)
=2(1+2)n-2n=2•3n-2n. …(4分)
(2)∵an=2n,bn=
ai,
∴bn=0+2+4+…+2n=n(n+1),
∴
(bi
)=1•2•
+2•3•
+3•4•
+…+n(n+1)
,
(1+x)n=
+
x+
x2+
x3+…+
xn,
两边同乘以x,则有x(1+x)n=
x+
x2+
x3+
x4+…+
xn+1,
两边求导,左边=(1+x)n+nx(1+x)n-1,
右边=
+2
x+3
x2+4
x3+…+(n+1)
xn,
即(1+x)n+nx(1+x)n-1=
+2
x+3
x2+4
x3+…+(n+1)
xn(*),
对(*)式两边再求导,
得2n(1+x)n-1+n(n-1)x(1+x)n-2=2•1•
+3•2•
x+4•3•
x2+…+(n+1)n
xn-1
取x=1,则有(n2+3n)•2n-2=1•2•
+2•3•
+3•4•
+…+n(n+1)
∴
(bi
)=(n2+3n)•2n-2.…(10分)
| n |
 |
| i=0 |
∴bn=20+21+22+…+2n=2n+1-1,
∴
| n |
 |
| i=0 |
| C | i n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
=21•
| C | 0 n |
| C | 0 n |
| C | 1 n |
| C | 1 n |
| C | 2 n |
| C | 2 n |
| C | n n |
| C | n n |
=2(
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
=2(1+2)n-2n=2•3n-2n. …(4分)
(2)∵an=2n,bn=
| n |
 |
| i=0 |
∴bn=0+2+4+…+2n=n(n+1),
∴
| n |
 |
| i=0 |
| C | i n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
(1+x)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
两边同乘以x,则有x(1+x)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
两边求导,左边=(1+x)n+nx(1+x)n-1,
右边=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
即(1+x)n+nx(1+x)n-1=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
对(*)式两边再求导,
得2n(1+x)n-1+n(n-1)x(1+x)n-2=2•1•
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
取x=1,则有(n2+3n)•2n-2=1•2•
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
∴
| n |
 |
| i=1 |
| C | i n |
点评:本题考查数列的前n项和的求法,综合性强,难度大,计算繁琐,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
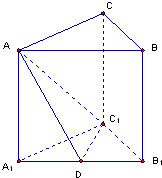 如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.
如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.