题目内容
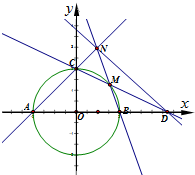 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.(1)求与直线AC垂直的圆的切线方程;
(2)设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N,
①若D点坐标为(2
| 3 |
②求证:2kND-kMB为定值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)先求直线AC的方程,设出切线方程,利用点线距离等于半径,即可求与直线AC垂直的圆的切线方程;
(2)①求出CM的方程,圆心到直线CM的距离,即可求弦CM的长;
②确定N,D的坐标,表示出2kND-kMB,即可证明2kND-kMB为定值.
(2)①求出CM的方程,圆心到直线CM的距离,即可求弦CM的长;
②确定N,D的坐标,表示出2kND-kMB,即可证明2kND-kMB为定值.
解答:
解:(1)由题意,A(-2,0),B(2,0),C(0,2),
∴直线AC:
+
=1,即x-y+2=0,…(2分)
设l:x+y+b=0,∴
=2,则b=±2
,
∴l:x+y±2
=0; …(5分)
(2)①CM:x+
y-2
=0,圆心到直线CM的距离d=
=
,
∴弦CM的长为2
=2 …(9分)
②设M(x0,y0),则x0≠±2,x0≠0,
+
=4,直线lCM:y=
x+2,
则D(
,0),kMB=
,直线lBM:y=
(x-2),
又lAC:y=x+2AC与BM交点N(
,
),kND=
=
将
=4-
,代入得kND=
,…(13分)
所以2kND-kMB=
-
=
,
得2kND-kMB=
=
=1为定值.…(16分)
∴直线AC:
| x |
| -2 |
| y |
| 2 |
设l:x+y+b=0,∴
| |b| | ||
|
| 2 |
∴l:x+y±2
| 2 |
(2)①CM:x+
| 3 |
| 3 |
2
| ||||
|
| 3 |
∴弦CM的长为2
| 4-3 |
②设M(x0,y0),则x0≠±2,x0≠0,
| x | 2 0 |
| y | 2 0 |
| y0-2 |
| x0 |
则D(
| 2x0 |
| 2-y0 |
| y0 |
| x0-2 |
| y0 |
| x0-2 |
又lAC:y=x+2AC与BM交点N(
| 4-2x0-2y0 |
| x0-y0-2 |
| -4y0 |
| x0-y0-2 |
| ||||
|
4y0-2
| ||||
|
将
| x | 2 0 |
| y | 2 0 |
| y0-2 |
| x0+y0-2 |
所以2kND-kMB=
| 2(y0-2) |
| x0+y0-2 |
| y0 |
| x0-2 |
x0y0-2y0-4x0+8-
| ||
|
得2kND-kMB=
x0y0-2y0-4x0+8-
| ||
4-
|
x0y0-2y0-4x0+8-
| ||
8-
|
点评:本题考查直线方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知a=12(16),b=25(7),c=33(4),则a,b,c的大小关系( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<c<a |
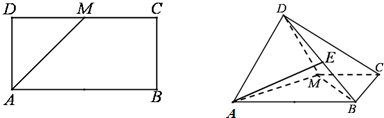 如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.