题目内容
6．在△ABC中，a=2，b=3，c=4，则其最大内角的余弦值为-$\frac{1}{4}$．分析 判断得到C为最大内角，利用余弦定理求出cosC的值即可．
解答 解：∵在△ABC中，a=2，b=3，c=4，
∴C为最大内角，
则cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{4+9-16}{12}$=-$\frac{1}{4}$，
故答案为：-$\frac{1}{4}$．
点评 此题考查了余弦定理，以及三角形的边角关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
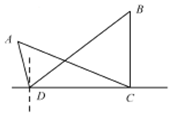如图所示，为了测量A、B处岛屿的距离，小明在D处观测，A、B分别在D处的北偏西15°、北偏东45°方向，再往正东方向行驶40海里至C处，观测B在C处的正北方向，A在C处的北偏西60°方向，则A、B两处岛屿的距离为20$\sqrt{6}$海里．
17．已知函数f（x）=x3-x+1，则曲线y=f（x）在点（0，1）处的切线与两坐标轴所围成的三角形的面积为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 2 |
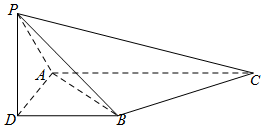如图，三棱锥P-ABC，侧棱PA=2，底面三角形ABC为正三角形，边长为2，顶点P在平面ABC上的射影为D，有AD⊥DB，且DB=1．
1．执行如图所示的程序框图，若输入a=-7，d=3，则输出的S为（ ）
| A． | S=-12 | B． | S=-11 | C． | S=-10 | D． | S=-6 |
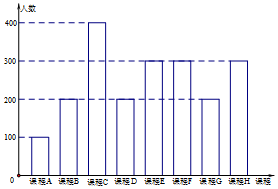为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查（调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程）．本次调查结果如下．图中，课程A，B，C，D，E为人文类课程，课程F，G，H为自然科学类课程．为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组M”）．
18．设函数f（x）满足2x2f（x）+x3f'（x）=ex，f（2）=$\frac{e^2}{8}$，则x∈[2，+∞）时，f（x）的最小值为（ ）
| A． | $\frac{e^2}{2}$ | B． | $\frac{{3{e^2}}}{2}$ | C． | $\frac{e^2}{4}$ | D． | $\frac{e^2}{8}$ |