题目内容
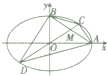 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
(1)用e表示点C、D的坐标.
(2)求证:
| S1 |
| S2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出直线OM的方程,代入椭圆方程,化简整理,即可用e表示点C、D的坐标.
(2)
=
=
,化简可得结论.
(2)
| S1 |
| S2 |
| |CM| |
| |DM| |
| ||||||||
|
解答:
(1)解:∵a=2,∴b2=a2(1-e2)=4(1-e2),
∴b=2
,
∴A(2,0),B(0,2
),
∴M(1,
),故直线OM的方程为y=
x,
代入椭圆方程,化简整理得:x2=
=2,即x=±
,
可得:C(
,
),
D(-
,-
).(6分)
(2)证明:
=
=
=
=3-2
,为定值.(12分)
∴b=2
| 1-e2 |
∴A(2,0),B(0,2
| 1-e2 |
∴M(1,
| 1-e2 |
| 1-e2 |
代入椭圆方程,化简整理得:x2=
| a2 |
| 2 |
| 2 |
可得:C(
| 2 |
| 2(1-e2) |
D(-
| 2 |
| 2(1-e2) |
(2)证明:
| S1 |
| S2 |
| |CM| |
| |DM| |
| ||||||||
|
=
| ||
|
| 2 |
点评:本题考查椭圆方程的求法,考查两个三角形面积比值是否为定值的判断与证明,属于中档题.

练习册系列答案
相关题目
 如图所示的茎叶图记录了甲、乙两组各四名同学的植树的棵数;乙组有一个数据模糊,用X表示.
如图所示的茎叶图记录了甲、乙两组各四名同学的植树的棵数;乙组有一个数据模糊,用X表示. 如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<
如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β< 将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)
将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)