题目内容
 将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)
将正整数按如图的规律排列,把第一行数1,2,3,10,17,…记为数列{an}(n∈N+),第一数列1,4,9,16,25,…记为数列{bn}(n∈N+)(1)写出数列{an},{bn}的通项公式;
(2)若数列{an},{bn}的前n项和分别为Sn,Tn,用数学归纳法证明:3(Tn+Tn)=2n3+4n(n∈N+);
(3)当n≥3时,证明:
| 5 |
| 4 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
| 7 |
| 4 |
考点:数列的求和,数列与不等式的综合,数学归纳法
专题:证明题,综合题,点列、递归数列与数学归纳法
分析:(1)依题意,可知an-an-1=2n-1,从而可求得an=a1+1+3+…+(2n-3)=n2-2n+2;观察知bn=n2;
(2)利用数学归纳法证明即可:当n=1时3(T1+S1)=2×13+4×1=6成立;假设n=k时等式成立,即3(Tk+Sk)=2k3+4k,去推证n=k+1时,3(Tk+1+Sk+1)=2(k+1)3+4(k+1)也成立即可;
(3)当n≥3时,bn=n2>0,易证
+
+…+
>
+
=
;利用放缩法易证
+
+…+
=
+
+
+…+
<
+
+
+
+…+
,再利用裂项法即可证得结论成立.
(2)利用数学归纳法证明即可:当n=1时3(T1+S1)=2×13+4×1=6成立;假设n=k时等式成立,即3(Tk+Sk)=2k3+4k,去推证n=k+1时,3(Tk+1+Sk+1)=2(k+1)3+4(k+1)也成立即可;
(3)当n≥3时,bn=n2>0,易证
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| b1 |
| 1 |
| b2 |
| 5 |
| 4 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 1 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1 |
| 1 |
| 22 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)n |
解答:
(本小题满分14分)
解:(1)由an-an-1=2n-1,得:an=a1+1+3+…+(2n-3)=n2-2n+2,…(3分)
bn=n2…(4分)
(2)①当n=1时,T1=S1=1,∴3(T1+S1)=6,又2n3+4n=6,∴n=1时等式成立;…(5分)
②假设n=k时等式成立,即3(Tk+Sk)=2k3+4k,
则n=k+1时,
3(Tk+1+Sk+1)=3(Tk+Sk)+3(bk+1+ak+1)=2k3+4k+3[(k+1)2+(k+1)2-2(k+1)+2]
=2k3+4k+6+6(k+1)2-6(k+1)
=2k(k2-1)+6(k+1)+6k(k+1)
=(2k2+4k+6)(k+1)
=[2(k+1)2+4](k+1)
=2(k+1)3+4(k+1),
∴n=k+1时等式也成立.…(8分)
根据①②,3(Tn+Sn)=2n3+4n(n∈N+);都成立. …(9分)
(3)当n≥3时,bn=n2>0,∴
+
+…+
>
+
=
.…(11分)
又
+
+…+
=
+
+
+…+
<
+
+
+
+…+
=
+(
-
)+(
-
)+…+(
-
)=
+
-
<
.
综上可知:综上可知:
<
+
+…+
<
成立.…(14分)
解:(1)由an-an-1=2n-1,得:an=a1+1+3+…+(2n-3)=n2-2n+2,…(3分)
bn=n2…(4分)
(2)①当n=1时,T1=S1=1,∴3(T1+S1)=6,又2n3+4n=6,∴n=1时等式成立;…(5分)
②假设n=k时等式成立,即3(Tk+Sk)=2k3+4k,
则n=k+1时,
3(Tk+1+Sk+1)=3(Tk+Sk)+3(bk+1+ak+1)=2k3+4k+3[(k+1)2+(k+1)2-2(k+1)+2]
=2k3+4k+6+6(k+1)2-6(k+1)
=2k(k2-1)+6(k+1)+6k(k+1)
=(2k2+4k+6)(k+1)
=[2(k+1)2+4](k+1)
=2(k+1)3+4(k+1),
∴n=k+1时等式也成立.…(8分)
根据①②,3(Tn+Sn)=2n3+4n(n∈N+);都成立. …(9分)
(3)当n≥3时,bn=n2>0,∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| b1 |
| 1 |
| b2 |
| 5 |
| 4 |
又
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 1 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 1 |
| 1 |
| 22 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n-1)n |
=
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| n |
| 7 |
| 4 |
综上可知:综上可知:
| 5 |
| 4 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 7 |
| 4 |
点评:本题考查数列的求和,着重考查数列的通项公式的确定及数学归纳法的应用,考查放缩法与裂项法的综合应用,考查推理、综合运算及抽象思维、逻辑思维能力,属于难题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
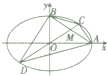 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E: 如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,
如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,