题目内容
 如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<
如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为d,再由点C沿东偏北β(β<| π |
| 2 |
(Ⅰ)若β=75°,求sin∠BCD的值;
(Ⅱ)求此建筑物的高度(用字母表示).
考点:解三角形的实际应用
专题:解三角形
分析:(Ⅰ)先求得∠BCD,在利用两角和公式求得sin∠BCD的值.
(Ⅱ)先求得∠CBD,进而利用正弦定理求得BC,最后在Rt△ABC中求得AB.
(Ⅱ)先求得∠CBD,进而利用正弦定理求得BC,最后在Rt△ABC中求得AB.
解答:
解:(Ⅰ)∠BCD=90°+75°=165°,
∴sin∠BCD=sin165°=sin(120°+45°)=
×
-
×
=
.
(Ⅱ)∠CBD=180°-165°-γ=15°-γ
在△BCD中,由正弦定理知
=
,
∴BC=
•sin∠BCD=
•
,
在Rt△ABC中,AB=BC•tan∠BCA=
•
•tand.
∴sin∠BCD=sin165°=sin(120°+45°)=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
(Ⅱ)∠CBD=180°-165°-γ=15°-γ
在△BCD中,由正弦定理知
| BC |
| sin∠BCD |
| CD |
| sin∠CBD |
∴BC=
| CD |
| sin∠CBD |
| d |
| sin(15°-γ) |
| ||||
| 4 |
在Rt△ABC中,AB=BC•tan∠BCA=
| d |
| sin(15°-γ) |
| ||||
| 4 |
点评:本题主要考查了解三角形的实际应用.考查了学生对基础知识的综合运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
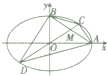 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E: 如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,
如图,AB为圆柱的底面直径,过母线的截面ACEF是边长为1的正方形,