题目内容
已知函数f(x)=ax3+bx2-2x在x=-2和x=1处取得极值
(1)求函数的解析式;
(2)求函数在[-2,2]上的最大值和最小值.
(1)求函数的解析式;
(2)求函数在[-2,2]上的最大值和最小值.
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出f(x)的导函数,利用极值点与导数的关系f′(x)=0,求出a、b的值;
(2)分别求出端点值和极值,通过比较得出该区间上的最值.
(2)分别求出端点值和极值,通过比较得出该区间上的最值.
解答:
解:(1)∵f(x)=ax3+bx2-2x,
∴f′(x)=3ax2+2bx-2;
由题意知f′(-2)=0,f′(1)=0,
∴
;
解得a=
,b=
;
∴f(x)=
x3+
x2-2x;
(2)由(1)可得,最值应在x=-2,1,2中取得
∵f(-2)=
×(-2)3+
×(-2)2-2×(-2)=
,
f(1)=
×13+
×12-2×1=-
,
f(2)=
×23+
×22-2×2=
,
∴函数f(x)在[-2,2]上的最大值为
,最小值为-
.
∴f′(x)=3ax2+2bx-2;
由题意知f′(-2)=0,f′(1)=0,
∴
|
解得a=
| 1 |
| 3 |
| 1 |
| 2 |
∴f(x)=
| 1 |
| 3 |
| 1 |
| 2 |
(2)由(1)可得,最值应在x=-2,1,2中取得
∵f(-2)=
| 1 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |
f(1)=
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 6 |
f(2)=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
∴函数f(x)在[-2,2]上的最大值为
| 10 |
| 3 |
| 7 |
| 6 |
点评:本题考查了利用导数研究函数的极值与最值的问题,求函数在闭区间上的最值时,应比较函数在区间内所有的极值与端点处的函数值,是中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知全集U={0,1,2},且∁UA={2},则集合A等于( )
| A、{0} | B、{1} |
| C、∅ | D、{0,1} |
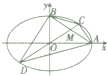 如图所示,已知A、B分别是离心率为e的椭圆E:
如图所示,已知A、B分别是离心率为e的椭圆E: