题目内容
1.已知椭圆的焦点在x轴上,椭圆上横坐标等于焦点横坐标的点,它到x轴的距离等于短半轴长的$\frac{2}{3}$,求椭圆的离心率.分析 设椭圆的方程,由题意,求得M坐标,利用勾股定理,及椭圆的定义,代入求得a和b的关系,利用椭圆的离心率公式即可求得椭圆的离心率.
解答 解:设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,(a>b>0),焦点坐标为(±c,0),
设M(x,y)在椭圆上,则P到x轴的距离等于短半轴长的$\frac{2}{3}$,
即x=c,y=$\frac{2}{3}$b,
Rt△MF1F2中,F1F2⊥MF2,
∴丨F1F2丨2+丨MF2丨2=丨MF1丨2,即4c2+$\frac{4}{9}$=丨MF1丨2,
根据椭圆的定义得:丨MF1丨+丨MF2丨=2a,
可得丨MF1丨2=(2a-丨MF2丨)2=(2a-$\frac{2}{3}$b)2,
∴(2a-$\frac{2}{3}$b)2=4c2+$\frac{4}{9}$b2,整理得4c2-4a2+$\frac{8}{3}$ab=0,
可得3(a2-c2)=2ab,
则3b2=2ab,则b=$\frac{2}{3}$a,
由题意的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{5}}{3}$,
椭圆的离心率$\frac{\sqrt{5}}{3}$.
点评 本题考查椭圆的标准方程及简单几何性质,椭圆的定义,考查计算能力,属于中档题.

练习册系列答案
相关题目
14.已知集合A={-3,-2,-1},B={x|(x-1)(x+2)≤0,x∈Z},则A∪B=( )
| A. | {-1} | B. | {-2,-1} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1,0,1} |
15.已知等比数列{an}的各项都为正数,且a3,$\frac{1}{2}{a_5},{a_4}$成等差数列,则$\frac{{{a_3}+{a_5}}}{{{a_4}+{a_6}}}$的值是( )
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
12.复数$\frac{2}{1+i}$的虚部是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
19.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为( )
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
13.某人吃完饭后散步,在0到3小时内速度与时间的关系为v=t3-3t2+2t(km/h),这3小时内他走过的路程为( )
| A. | $\frac{9}{4}km$ | B. | $\frac{10}{4}km$ | C. | $\frac{11}{4}km$ | D. | $\frac{13}{4}km$ |
10.若sinθ+cosθ=$\sqrt{2}$,则tanθ+$\frac{1}{tanθ}$=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
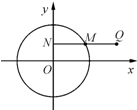 如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.
如图,已知点M在圆O:x2+y2=4上运动,MN⊥y轴(垂足为N),点Q在NM的延长线上,且|QN|=2|MN|.