题目内容
10．若sinθ+cosθ=$\sqrt{2}$，则tanθ+$\frac{1}{tanθ}$=（ ）| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
分析 利用同角三角函数的基本关系，求得要求式子的值．
解答 解：∵sinθ+cosθ=$\sqrt{2}$，两边平方可得1+2sinθcosθ=2，
即sinθcosθ=$\frac{1}{2}$，
则tanθ+$\frac{1}{tanθ}$=$\frac{sinθ}{cosθ}$+$\frac{cosθ}{sinθ}$=$\frac{1}{sinθcosθ}$=2，
故选：D．
点评 本题主要考查同角三角函数的基本关系，属于基础题．
练习册系列答案
相关题目
3．
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题：
“今有蒲生一日，长三尺．莞生一日，长一尺．蒲生日自半．莞生日自倍．问几何日而长等？”（蒲常指一种多年生草本植物，莞指水葱一类的植物）
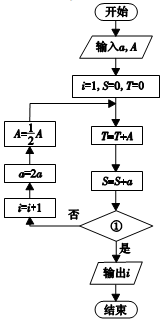
现欲知几日后，莞高超过蒲高一倍．为了解决这个新问题，设计右面的程序框图，输入A=3，a=1．那么在①处应填（ ）
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题：“今有蒲生一日，长三尺．莞生一日，长一尺．蒲生日自半．莞生日自倍．问几何日而长等？”（蒲常指一种多年生草本植物，莞指水葱一类的植物）
现欲知几日后，莞高超过蒲高一倍．为了解决这个新问题，设计右面的程序框图，输入A=3，a=1．那么在①处应填（ ）
| A． | T＞2S？ | B． | S＞2T？ | C． | S＜2T？ | D． | T＜2S？ |
5．甲、乙、丙、丁、戊5名学生各自在3门数学选修课：数学史、数学建模和几何画板中任选一门学习，则这三门课程都有同学选修且甲不选修几何画板的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{96}{125}$ | C． | $\frac{32}{81}$ | D． | $\frac{100}{243}$ |
15．设抛物线y2=2px的焦点在直线2x+3y-4=0上，则该抛物线的准线方程为（ ）
| A． | x=-1 | B． | x=-2 | C． | x=-3 | D． | x=-4 |
20．已知集合A={1，2，3，4，5}，B={x∈Z|x≤2}，则A∩B中的元素个数为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |