题目内容
11.已知五边形ABCDE满足AB=BC=CD=DE,∠BAE=∠AED=90°,∠BCD=120°,若F为线段AE的中点,则往五边形ABCDE内投掷一点,该点落在△BDF内的概率为$\frac{2}{5}$.分析 分别求出△BDF、五边形ABCDE的面积,一面积为测度,即可得出结论.
解答 解:由题意,ABDF为长方形,设AB=1,则BD=$\sqrt{3}$,S△BDF=$\frac{1}{2}×\sqrt{3}×1$=$\frac{\sqrt{3}}{2}$,
五边形ABCDE的面积S=1×$\sqrt{3}$+$\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$,
∴往五边形ABCDE内投掷一点,该点落在△BDF内的概率为$\frac{\frac{\sqrt{3}}{2}}{\frac{5\sqrt{3}}{4}}$=$\frac{2}{5}$,
故答案为$\frac{2}{5}$.
点评 此题考查了几何概率的求法,利用面积比计算出几何概率,根据题意求出五边形的面积比是解本题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
3.已知f(x)=$\left\{\begin{array}{l}{2^x}+1,x<1\\-{x^2}+ax,x≥1\end{array}$,若f(x)的值域为(-∞,3),则实数a的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | $[-2\sqrt{3},-2)∪(2,2\sqrt{3}]$ | C. | $[2,2\sqrt{3})$ | D. | [2,+∞) |
20.已知集合A={1,2,3,4,5},B={x∈Z|x≤2},则A∩B中的元素个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.设集合A={x|(x-3)(x-1)>0},B={x|y=lg(2x-3)},则A∩B=( )
| A. | $[\frac{3}{2},3)$ | B. | (3,+∞) | C. | $(1,\frac{3}{2})$ | D. | ($\frac{3}{2}$,3) |
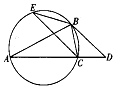 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.