��Ŀ����
6��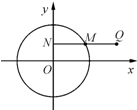 ��ͼ����֪��M��ԲO��x2+y2=4���˶���MN��y�ᣨ����ΪN������Q��NM���ӳ����ϣ���|QN|=2|MN|��
��ͼ����֪��M��ԲO��x2+y2=4���˶���MN��y�ᣨ����ΪN������Q��NM���ӳ����ϣ���|QN|=2|MN|��������Q�Ĺ켣���̣�
����ֱ��l��y=$\frac{1}{2}$x+m�루���ж���Q�Ĺ켣����������ͬ�ĵ�A��B��ԲO�ϴ�������C��D������|CA|=|CB|��|DA|=|DB|��
��������m��ȡֵ��Χ��
��������$\frac{|CD|}{|AB|}$ȡ����Сֵʱֱ��l�ķ��̣�
���� ������M��x0��y0����حQNح=2حMNح����x=2x0��y=2y0������Բ�ķ��̣�������ö���Q�Ĺ켣���̣�
��������������Բ���̣��ɡ���0�����m��ȡֵ��Χ������Τ�ﶨ�����е����깫ʽ����|CA|=|CB|��|DA|=|DB|���������m��ȡֵ��Χ��
���������ҳ���ʽ�����حABح��ֱ��2x+y+$\frac{3m}{2}$=0��Բ���ཻ��حCDح�����$\frac{|CD|}{|AB|}$�ı���ʽ�����$\frac{|CD|}{|AB|}$����Сֵ���������m��ֵ�����ֱ��l�ķ��̣�
��� �⣺�����趯��Q��x��y������M��x0��y0����
�ɵ�M��x0��y0����Բx2+y2=4�ϣ���x02+y02=4��
��حQNح=2حMNح����x=2x0��y=2y0��
��x0=$\frac{x}{2}$��y0=y����x02+y02=4��
�ö���Q�Ĺ켣����Ϊ$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$����4�֣�
������������ֱ��l�루���еĹ켣���̵�$\left\{\begin{array}{l}{y=\frac{1}{2}x+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$��
��x2+2mx+2m2-8=0����������������A��B���ʡ���0�����حmح��2$\sqrt{2}$���٣�5�֣�
��A��x1��y1����B��x1��y1����AB���е�E��x��y�����ɸ���ϵ���Ĺ�ϵ��x1+x2=-m��$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}=-m}\\{y=\frac{1}{2}����-m��+m=\frac{m}{2}}\end{array}\right.$
��$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}=-m}\\{y=\frac{1}{2}����-m��+m=\frac{m}{2}}\end{array}\right.$��
��AB�Ĵ�ֱƽ���߷���Ϊy-$\frac{m}{2}$=-2��x+m������2x+y+$\frac{3m}{2}$=0����6�֣�
��ԲO�ϴ�������C��D������حCAح=حCBح��حDAح=حDBح��
��֪AB�Ĵ�ֱƽ������ԲO����C��D���㣬��ֱ����Բ��λ�ù�ϵ�ɵ�$\frac{ح\frac{3m}{2}ح}{\sqrt{5}}$��2��
��ã�حmح��$\frac{4\sqrt{5}}{3}$����
�ɢ١��ڽ��حmح��2$\sqrt{2}$��
��m��ȡֵ��Χ��-2$\sqrt{2}$��m��2$\sqrt{2}$����8�֣�
�������ɣ�����֪$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-2m}\\{{x}_{1}{x}_{2}=2{m}^{2}-8}\end{array}\right.$��
��حABح=$\sqrt{1+{k}^{2}}$•حx1-x2ح=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$��
=$\sqrt{1+��\frac{1}{2}��^{2}}$•$\sqrt{4{m}^{2}-4��2{m}^{2}-8��}$=$\frac{\sqrt{5}}{2}$��$\sqrt{32-4{m}^{2}}$����9�֣�
��ֱ��2x+y+$\frac{3m}{2}$=0��Բ���ཻ��حCDح=2$\sqrt{{2}^{2}-��\frac{ح\frac{3m}{2}ح}{\sqrt{5}}��^{2}}$=2$\sqrt{\frac{80-9{m}^{2}}{20}}$����10�֣�
��$\frac{حCDح}{حABح}$=$\frac{2\sqrt{\frac{80-9{m}^{2}}{20}}}{\frac{\sqrt{5}}{2}��\sqrt{32-4{m}^{2}}}$=$\frac{2}{5}$•$\sqrt{\frac{80-9{m}^{2}}{32-4{m}^{2}}}$=$\frac{2}{5}$•$\sqrt{\frac{9}{4}+\frac{2}{8-{m}^{2}}}$��
�ɣ�����-2$\sqrt{2}$��m��2$\sqrt{2}$���ʵ�m=0ʱ��$\frac{حCDح}{حABح}$=$\frac{2}{5}$•$\sqrt{\frac{9}{4}+\frac{2}{8-{m}^{2}}}$��ȡ����Сֵ����11�֣�
��ֱ��l����Ϊy=$\frac{1}{2}$x����12�֣�
���� ���⿼��켣���̵���������Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����ҳ���ʽ����������������������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 12 |
| A�� | 0 | B�� | 504 | C�� | 1008 | D�� | 2016 |
| A�� | x=-1 | B�� | x=-2 | C�� | x=-3 | D�� | x=-4 |
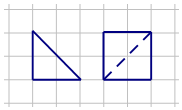 ��ͼ������ֽ��С�����εı߳�Ϊ1������������ij�����������ͼ������ֱ�������Σ��Ͳ���ͼ���Ҹü���������Ϊ$\frac{8}{3}$����ü�����ĸ���ͼ�����ǣ�������
��ͼ������ֽ��С�����εı߳�Ϊ1������������ij�����������ͼ������ֱ�������Σ��Ͳ���ͼ���Ҹü���������Ϊ$\frac{8}{3}$����ü�����ĸ���ͼ�����ǣ�������


