题目内容
19．《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P-ABC为鳖臑，PA⊥平面ABC，PA=AB=2，AC=4，三棱锥P-ABC的四个顶点都在球O的球面上，则球O的表面积为（ ）| A． | 8π | B． | 12π | C． | 20π | D． | 24π |
分析 由题意，PC为球O的直径，求出PC，可得球O的半径，即可求出球O的表面积．
解答 解：由题意，PC为球O的直径，PC=$\sqrt{4+16}$=2$\sqrt{5}$，
∴球O的半径为$\sqrt{5}$，
∴球O的表面积为4π•5=20π，
故选C．
点评 本题考查球O的表面积，考查学生的计算能力，求出球的半径是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．在△ABC中，角A，B，C所对的边分别为a，b，c，已知2a-b=2ccosB，则角C的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
7．已知$\overrightarrow a$，$\overrightarrow b$为单位向量，其夹角为120°，则$（\overrightarrow a-2\overrightarrow b）•\overrightarrow b$=（ ）
| A． | $-\frac{5}{2}$ | B． | $-\frac{3}{2}$ | C． | -1 | D． | 2 |
14．已知tanθ=2，且θ∈$（{0，\frac{π}{2}}）$，则cos2θ=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{4}{5}$ |
8．直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左支、右支分别交于A、B两点，O为坐标原点，且△AOB为等腰直角三角形，则该双曲线的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{30}}{5}$ | D． | $\frac{3\sqrt{5}}{5}$ |
5．甲、乙、丙、丁、戊5名学生各自在3门数学选修课：数学史、数学建模和几何画板中任选一门学习，则这三门课程都有同学选修且甲不选修几何画板的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{96}{125}$ | C． | $\frac{32}{81}$ | D． | $\frac{100}{243}$ |
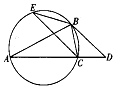如图，已知△ABC内接于圆，AB=AC，过点B作此圆的切线，与AC的延长线交于点D，且BD=2CD．