题目内容
6.已知映射f:A→B,A={1,3},B={a,b},a,b是实数,对应法则f:x→x2,则a+b的值是10.分析 据映射的定义中,A中任意一个元素在B中都有唯一的一个元素和它对应,即可求出a,b的值.
解答 解:映射f:A→B,A={1,3},B={a,b},a,b是实数,对应法则f:x→x2,
则a=12=1,b=32=9,
故a+b=10,
故答案为:10
点评 本题考查的知识点是映射的定义,熟练掌握映射定义中A中元素的任意性,和B中元素的唯一性是解答本题的关键.

练习册系列答案
相关题目
1.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则φ=( )
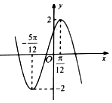

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
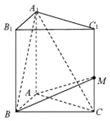 直三棱柱ABC-A1B1C1中,底面ABC为等腰三角形,AB⊥AC,AB=AC=2,AA1=4,M是侧棱CC1上一点,设MC=h.
直三棱柱ABC-A1B1C1中,底面ABC为等腰三角形,AB⊥AC,AB=AC=2,AA1=4,M是侧棱CC1上一点,设MC=h.