题目内容
18.设f(x)=lg(5-x).(1)若10f(k)=10f(2)×10f(3),求k的值;
(2)若f(2m-1)<f(m+1),求实数m的取值范围.
分析 (1)由10f(k)=10f(2)×10f(3),可得f(k)=f(2)+f(3),即lg(5-k)=lg3+lg2.再利用对数的运算法则即可得出.
(2)由f(x)=lg(5-x)单调递减.f(2m-1)<f(m+1),可得2m-1>m+1,5-(2m-1)>0,5-(m+1)>0,解得m范围.
解答 解:(1)∵10f(k)=10f(2)×10f(3),∴f(k)=f(2)+f(3),
∴lg(5-k)=lg3+lg2,∴5-k=2×3,解得k=-1.
经过验证满足条件.
∴k=-1.
(2)∵f(x)=lg(5-x)单调递减.f(2m-1)<f(m+1),
∴2m-1>m+1,5-(2m-1)>0,5-(m+1)>0,
解得2<m<3.
点评 本题考查了指数与对数的运算法则、指数函数与对数函数的单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8.函数$f(x)={sin^2}x+\sqrt{3}sinxcosx$在区间$[{\frac{π}{4},\frac{π}{2}}]$上的最小值为( )
| A. | 1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1+\sqrt{3}$ |
3.汉中最美油菜花节期间,5名游客到四个不同景点游览,每个景点至少有一人,则不同的游览方法共有( )种.
| A. | 120 | B. | 625 | C. | 240 | D. | 1024 |
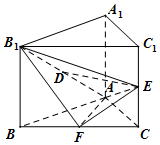 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.