设复数z=.若|z|≤1.则y≥x的概率为$\frac{1}{4}-\frac{1}{2π}$．题目和参考答案——青夏教育精英家教网—

题目内容

8．设复数z=（x-1）+yi（x，y∈R），若|z|≤1，则y≥x的概率为$\frac{1}{4}-\frac{1}{2π}$．

分析判断复数对应点图及内部部分．y≥x的图形是图形中阴影部分，根据几何概率的公式计算即可．

解答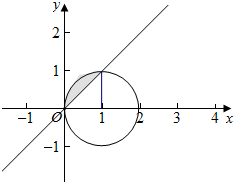解：复数z=（x-1）+yi（x，y∈R），|z|≤1，
∴（x-1）²+y²≤1，
∴（x，y）在以（1，0）为圆心，以1为半径的圆的上和圆的内部的点，
复数对应点图及内部部分，y≥x的图形是图形中阴影部分，
圆的面积为S=π，
S_阴影=$\frac{1}{4}$π-$\frac{1}{2}$，
∴则y≥x的概率为P=$\frac{{S}_{阴影}}{S}$=$\frac{\frac{1}{4}π-\frac{1}{2}}{π}$=$\frac{1}{4}-\frac{1}{2π}$，
故答案为：$\frac{1}{4}-\frac{1}{2π}$．

点评本题考查了几何概型的概率的求法，关键是求出阴影部分的面积，属于中档题．

练习册系列答案

19．已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x²，当x＞0时，f（x+1）=f（x）+f（1），若直线y=kx与函数y=f（x）的图象恰有11个不同的公共点，则实数k的取值范围为（$2\sqrt{6}-4$，$4\sqrt{3}-6$）．

16．使奇函数$f（x）=\sqrt{3}sin（2x+θ）+cos（2x+θ）$在$[0，\frac{π}{4}]$上为增函数的θ值为（　　）

3．已知函数f（x）=ln²x-2aln（ex）+3，x∈[e^-1，e²]
（1）当a=1时，求函数f（x）的值域；
（2）若f（x）≤-alnx+4恒成立，求实数a的取值范围．

13．下列说法正确的是③④⑤（填上所有正确说法的序号）
①残差平方和越大的模型，拟合效果越好；②用相关指数R²来刻画回归效果时，R²越小，说明模型的拟合效果越好；③在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适，这样的带状区域的宽度越窄，模型拟合精度越高．
④一个样本的方差${s^2}=\frac{1}{20}[{{{（{{x_1}-3}）}^2}+{{（{{x_2}-3}）}^2}+…{{（{{x_n}-3}）}^2}}]$，则这组数据等总和等于60；
⑤数据a₁，a₂，a₃，…，a_n的方差为σ²，则数据2a₁+1，2a₂+1，…2a_n+1的方差为4σ²．

20．设函数$f（x）=ax-\frac{b}{x}$，曲线y=f（x）在点（1，f（1））处的切线方程为3x-y-4=0．
（Ⅰ）求f（x）的解析式；
（Ⅱ）证明：曲线f（x）上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值．

17．抛物线x²=2py（p＞0）的焦点F，其准线与双曲线$\frac{x^2}{3}-\frac{y^2}{3}=1$相交于A，B两点，若△ABC是等边三角形，则p等于（　　）

	A．	向量$\overrightarrow{AB}$∥$\overrightarrow{CD}$就是$\overrightarrow{AB}$所在的直线平行于$\overrightarrow{CD}$所在的直线
	B．	共线向量是在一条直线上的向量
	C．	长度相等的向量叫做相等向量
	D．	零向量长度等于0

试题分类