题目内容
12.若函数y=f(x)(x∈R)满足f(x+4)=f(x),且当x∈[0,4]时,f(x)=1-$\frac{1}{2}$|x-2|,那么函数f(x)的图象与函数g(x)=$\left\{\begin{array}{l}{lg|x|,x<0}\\{|lgx|,x>0}\end{array}\right.$的图象的交点个数共有( )| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
分析 由题意可得f(x)为周期为4的函数,画出f(x)在(0,4)的图象,左右平移,再画出g(x)的图象,运用数形结合的方法,即可得到所求交点的个数.
解答  解:由f(x+4)=f(x),
解:由f(x+4)=f(x),
可得f(x)的周期为4,
作出当x∈[0,4]时,f(x)=1-$\frac{1}{2}$|x-2|的图象,
并将图象左右平移4k个单位(k为正整数),
画出g(x)的图象,
由图象可得在(0,4)内,有2个交点;在(4,8)内,有2个交点;
在(8,12)内有1个交点;在(-4,0)内有1个交点;
在(-8,-4)内有2个交点;在(-12,-8)内有1个交点.
即有f(x)与g(x)的图象共有9个交点.
故选:D.
点评 本题考查函数的周期性的运用,考查对数函数的图象和性质,运用数形结合的思想方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.过点($\sqrt{3}$,-1)且与圆x2+y2=4相切的直线方程是( )
| A. | $\sqrt{3}$x+y-4=0 | B. | x-$\sqrt{3}$y-4=0 | C. | x-$\sqrt{3}$y-2=0 | D. | $\sqrt{3}$x-y-4=0 |
3.1+2i+3i2+…+2005i2004的值是( )
| A. | -1000-1000i | B. | -1002-1002i | C. | 1003-1002i | D. | 1005-1000i |
20.与圆(x-2)2+y2=1相切且在两坐标轴上截距相等的直线共有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
4.已知m∈R,则函数f(x)=3x+m-2有零点的一个充分不必要条件为( )
| A. | 0<m<1 | B. | m<2 | C. | m<3 | D. | 0<m<3 |
7.已知F1,F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,过F1的直线与椭圆相交于A,B两点,若∠BAF2=60°,|AB|=|AF2|,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
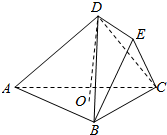 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.