题目内容
2.过点($\sqrt{3}$,-1)且与圆x2+y2=4相切的直线方程是( )| A. | $\sqrt{3}$x+y-4=0 | B. | x-$\sqrt{3}$y-4=0 | C. | x-$\sqrt{3}$y-2=0 | D. | $\sqrt{3}$x-y-4=0 |
分析 点($\sqrt{3}$,-1)是圆x2+y2=4上的一点,然后直接代入过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2求得圆的切线方程.
解答 解:∵把点($\sqrt{3}$,-1)代入圆x2+y2=4成立,
∴可知点($\sqrt{3}$,-1)是圆x2+y2=4上的一点,
则过($\sqrt{3}$,-1)的圆x2+y2=4的切线方程为$\sqrt{3}$x-y=4,
即$\sqrt{3}$x-y-4=0.
故选:D.
点评 本题考查圆的切线方程,过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2,此题是基础题.

练习册系列答案
相关题目
7.已知点P(x,y)在圆x2+y2-4x-2y+4=0上,则$\frac{y}{x}$的最大值和最小值分别是( )
| A. | 1,$\frac{1}{3}$ | B. | $\frac{4}{3}$,0 | C. | $\frac{4}{3}$,-$\frac{4}{3}$ | D. | 2,2 |
14.若函数y=f(x)在x=a处的导数为A,则$\underset{lim}{△x→0}$$\frac{f(a+△x)-f(a-△x)}{△x}$为( )
| A. | A | B. | 2A | C. | $\frac{A}{2}$ | D. | 0 |
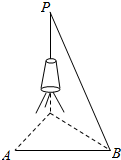 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.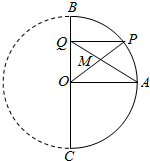 如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.
如图,BC是半圆的直径,O是圆心,OA是与BC垂直的圆的半径,P为半圆上一点(P与A、B、C不重合).过P向BC作垂线,垂足为Q.OP和AQ的交点为M.试问:当P移动时,M的轨迹是怎样的曲线?说明理由.