题目内容
已知数列{an}满足a1+a2+…+an=
an+1(n∈N*),数列{bn}为等比数列,a1=b1=2,a2=b2
(Ⅰ)求{an}、{bn}的 通项公式.
(Ⅱ)若对每个正整数k,在bk和bk+1之间插入ak个2,得到一个新数列{cn}.设Tn是数列{cn}的前n项和,试求满足Tm=2cm+1的所有正整数m.
| n |
| 2 |
(Ⅰ)求{an}、{bn}的 通项公式.
(Ⅱ)若对每个正整数k,在bk和bk+1之间插入ak个2,得到一个新数列{cn}.设Tn是数列{cn}的前n项和,试求满足Tm=2cm+1的所有正整数m.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由式子求出a2,由题意求出公比,根据等比数列的通项公式求出bn,利用递推公式和累积法求出an;
(Ⅱ)由(Ⅰ)知bn=2n,ak=2k,由已知写出c1=a1=2,c2=c3=2,c4=a2=4,c5=c6=c7=c8=2,c9=a3=8,…,讨论m=1、2,m≥3,求出Tm、2cm+1,列出方程并整理,讨论方程的解,从而得到结论.
(Ⅱ)由(Ⅰ)知bn=2n,ak=2k,由已知写出c1=a1=2,c2=c3=2,c4=a2=4,c5=c6=c7=c8=2,c9=a3=8,…,讨论m=1、2,m≥3,求出Tm、2cm+1,列出方程并整理,讨论方程的解,从而得到结论.
解答:
解:(Ⅰ)由题意知,a1=2,a1+a2+…+an=
an+1(n∈N*),
所以a1=
a2,解得a2=4,
因为数列{bn}为等比数列,a1=b1=2,a2=b2,
所以数列{bn}的公比是2,即bn=2•2n-1=2n,
由a1+a2+…+an=
an+1(n∈N*)得,
当n≥2时,a1+a2+…+an-1=
an(n∈N*),
两个式子相减得,an=
an+1-
an,即
=
,
当n=1时,
=
=2符合上式,
当n≥2时,
=
,
=
,
=
,…,
=
,
以上n-1个式子相乘得,
=
,所以an=2n;
(Ⅱ)由(Ⅰ)知,bn=2n,ak=2k,
由题意知,c1=a1=2,c2=c3=2,c4=a2=4,c5=c6=c7=c8=2,c9=a3=8,…,
则当m=1时,T1≠2c2,不合题意,当m=2时,T2=2c3,适合题意.
当m≥3时,若cm+1=2,则Tm≠2cm+1一定不适合题意,
从而cm+1必是数列{bn}中的某一项bk+1,
则Tm=b1+2+2+b2+2+2+2+2+b3+2+…+2+b4+2+…+b5+2+…+b6+…+bk-1+2+…+bk,
=(2+22+23+…+2k)+2(2+4+…+2k)
=2×(2k-1)+k(2+2k)=2k+1+2k2+2k-2,
又2cm+1=2bk+1=2×2k+1,
∴2k+1+2k2+2k-2=2×2k+1,即2k-k2-k+1=0,∴2k+1=k2+k,
∵2k+1为奇数,k2+k=k(k+1)为偶数,∴上式无解.
即当m≥3时,Tm≠2cm+1,
综上知,满足题意的正整数只有m=2.
| n |
| 2 |
所以a1=
| 1 |
| 2 |
因为数列{bn}为等比数列,a1=b1=2,a2=b2,
所以数列{bn}的公比是2,即bn=2•2n-1=2n,
由a1+a2+…+an=
| n |
| 2 |
当n≥2时,a1+a2+…+an-1=
| n-1 |
| 2 |
两个式子相减得,an=
| n |
| 2 |
| n-1 |
| 2 |
| an+1 |
| an |
| n+1 |
| n |
当n=1时,
| a2 |
| a1 |
| 4 |
| 2 |
当n≥2时,
| a2 |
| a1 |
| 2 |
| 1 |
| a3 |
| a2 |
| 3 |
| 2 |
| a4 |
| a3 |
| 4 |
| 3 |
| an |
| an-1 |
| n |
| n-1 |
以上n-1个式子相乘得,
| an |
| a1 |
| n |
| 1 |
(Ⅱ)由(Ⅰ)知,bn=2n,ak=2k,
由题意知,c1=a1=2,c2=c3=2,c4=a2=4,c5=c6=c7=c8=2,c9=a3=8,…,
则当m=1时,T1≠2c2,不合题意,当m=2时,T2=2c3,适合题意.
当m≥3时,若cm+1=2,则Tm≠2cm+1一定不适合题意,
从而cm+1必是数列{bn}中的某一项bk+1,
则Tm=b1+2+2+b2+2+2+2+2+b3+2+…+2+b4+2+…+b5+2+…+b6+…+bk-1+2+…+bk,
=(2+22+23+…+2k)+2(2+4+…+2k)
=2×(2k-1)+k(2+2k)=2k+1+2k2+2k-2,
又2cm+1=2bk+1=2×2k+1,
∴2k+1+2k2+2k-2=2×2k+1,即2k-k2-k+1=0,∴2k+1=k2+k,
∵2k+1为奇数,k2+k=k(k+1)为偶数,∴上式无解.
即当m≥3时,Tm≠2cm+1,
综上知,满足题意的正整数只有m=2.
点评:本题考查等比数列的通项公式,累积法求出数列的通项公式,等差、等比数列的前n项和公式,数列的求和方法:分组求和,同时考查逻辑推理能力,属于综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设随机变量X等可能地取值1,2,3,…,10,则P(X<6)的值为( )
| A、0.3 | B、0.5 |
| C、0.6 | D、0.2 |
若焦距为4的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为( )
A、4
| ||
B、2
| ||
| C、4 | ||
| D、2 |
若曲线C1:x2+y2-4x=0与曲线C2:y(y-mx-x)=0有四个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
 已知AB是圆O的直径,P是上半圆上的任意一点,PC是∠APB的平分线,E是下半圆的中点.
已知AB是圆O的直径,P是上半圆上的任意一点,PC是∠APB的平分线,E是下半圆的中点.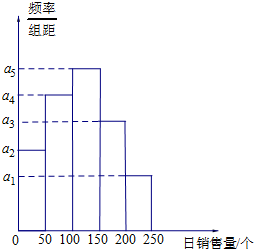 广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).