题目内容
（1）利用诱导公式求sin780°•cos（-420°）+sin（-330°）•cos（-300°）的值；
（2）求cos40°（1+
tan10°）的值．
（2）求cos40°（1+
| 3 |
考点：运用诱导公式化简求值,三角函数的化简求值
专题：三角函数的求值
分析：（1）由条件利用诱导公式求得所给式子的值．
（2）化切为弦，把要求的式子转化为
•（cos10°+
sin10°），再由三角函数的和（差）公式把原式等价转化
•2cos40°，由此能求出结果．
（2）化切为弦，把要求的式子转化为
| cos40° |
| cos10° |
| 3 |
| cos40° |
| cos10° |
解答：
解：（1）sin780°•cos（-420°）+sin（-330°）•cos（-300°）=sin60°cos（-60°）+sin30°cos60°=
×
+
×
=
．
（2）求cos40°（1+
tan10°）=cos40°（1+
•
）=
•（cos10°+
sin10°）=
•2cos40°=
=1
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
（2）求cos40°（1+
| 3 |
| 3 |
| sin10° |
| cos10° |
| cos40° |
| cos10° |
| 3 |
| cos40° |
| cos10° |
| sin80° |
| cos10° |
点评：本题考查三角函数的化简求值，解题时要认真审题，仔细求解，注意三角函数恒等变换的合理运用，属于基础题．
练习册系列答案
相关题目
已知椭圆
+
=1的左、右焦点分别为F1，F2，P为椭圆上一点，当|PF1|=λ|PF2|时λ的取值范围（ ）
| x2 |
| 9 |
| y2 |
| 8 |
| A、[1，3] | ||
| B、[1，2] | ||
C、[
| ||
D、[
|
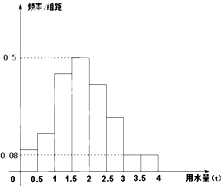为了解某社区家庭的月均用水量（单位：吨），现从该社区随机抽查100户，获得每户某年的月均用水量，并制作了频率分布表和频率分布直方图（如图）．