题目内容
已知中心在原点的双曲线的渐近线方程是y=±
x,且双曲线过点(
,
)
(Ⅰ)求双曲线的方程;
(Ⅱ)过双曲线右焦点F作倾斜角为
的直线交双曲线于A,B,求|AB|.
| 3 |
| 2 |
| 3 |
(Ⅰ)求双曲线的方程;
(Ⅱ)过双曲线右焦点F作倾斜角为
| π |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设双曲线方程为:3x2-y2=λ,点(
,
)代入,即可求双曲线的方程;
(Ⅱ)直线AB的方程与双曲线方程联立,利用韦达定理及弦长公式,即可求|AB|.
| 2 |
| 3 |
(Ⅱ)直线AB的方程与双曲线方程联立,利用韦达定理及弦长公式,即可求|AB|.
解答:
解:(Ⅰ)设双曲线方程为:3x2-y2=λ,点(
,
)代入得:λ=3,
所以所求双曲线方程为:x2-
=1…(6分)
(Ⅱ)直线AB的方程为:y=x-2,
由
得:2x2+4x-7=0,…(10分)
∴|AB|=
|x1-x2|=
•
=6.…(12分)
| 2 |
| 3 |
所以所求双曲线方程为:x2-
| y2 |
| 3 |
(Ⅱ)直线AB的方程为:y=x-2,
由
|
∴|AB|=
| 1+k2 |
| 2 |
| ||
| 2 |
点评:本题考查双曲线方程,考查直线与双曲线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
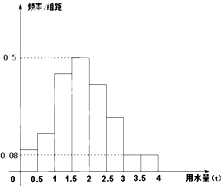 为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
 如图,在四面体PABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
如图,在四面体PABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.