题目内容
已知无穷数列{an]满足：a1=1，2a2=a1+a3，且对于任意n∈N*，都有an＞0，a2n+1=anan+2+4．
（1）求a2，a3，a4的值；
（2）求数列{an}的通项公式．
（1）求a2，a3，a4的值；
（2）求数列{an}的通项公式．
考点：数列递推式
专题：等差数列与等比数列
分析：（1）由已知条件，令n=1，得a22=a1a3+4，令n=2，得a32=a2a4+4，由此能求出a2，a3，a4的值．
（2）由an+12=anan+2+4，得an+22=an+1an+3+4，由此推导出数列{
}为常数数列从而能求出an=2n-1．
（2）由an+12=anan+2+4，得an+22=an+1an+3+4，由此推导出数列{
| an+an+2 |
| an+1 |
解答：
解：（1）由条件，?n∈N*，an+12=anan+2+4，
令n=1，得a22=a1a3+4．…（2分）
又∵2a2=a1+a3，且a1=1，解得a2=3，a3=5．…（4分）
再令n=2，得a32=a2a4+4，解得a4=7． …（6分）
（2）∵an+12=anan+2+4，①
∴an+22=an+1an+3+4，②
由①-②得，an+12-an+22=（anan+2+4）-（an+1an+3+4）
=anan+2-an+1an+3 …（8分）
∴an+12+an+1an+3=an+22+anan+2，
∴an+1（an+1+an+3）=an+2（an+an+2），
∴
=
，∴数列{
}为常数数列．…（12分）
∴
=
=2，
∴an+an+2=2an+1，
∴数列{an}为等差数列． …（14分）
又公差d=a2-a1=2，∴an=2n-1．…（16分）
令n=1，得a22=a1a3+4．…（2分）
又∵2a2=a1+a3，且a1=1，解得a2=3，a3=5．…（4分）
再令n=2，得a32=a2a4+4，解得a4=7． …（6分）
（2）∵an+12=anan+2+4，①
∴an+22=an+1an+3+4，②
由①-②得，an+12-an+22=（anan+2+4）-（an+1an+3+4）
=anan+2-an+1an+3 …（8分）
∴an+12+an+1an+3=an+22+anan+2，
∴an+1（an+1+an+3）=an+2（an+an+2），
∴
| an+an+2 |
| an+1 |
| an+1+an+3 |
| an+2 |
| an+an+2 |
| an+1 |
∴
| an+an+2 |
| an+1 |
| a1+a3 |
| a2 |
∴an+an+2=2an+1，
∴数列{an}为等差数列． …（14分）
又公差d=a2-a1=2，∴an=2n-1．…（16分）
点评：本题考查数列中前4项的求法，考查数列的通项公式的求法，解题时要认真审题，注意构造法的合理运用．
练习册系列答案
相关题目
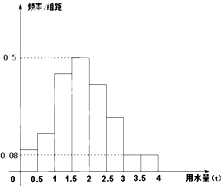为了解某社区家庭的月均用水量（单位：吨），现从该社区随机抽查100户，获得每户某年的月均用水量，并制作了频率分布表和频率分布直方图（如图）．