题目内容
已知a>0,f(logax)=
(x-x-1).
(1)求f(x)的解析式;
(2)判断f(x)的奇偶性与单调性;
(3)对于f(x),当x∈(-1,1)时,f(1-m)+f(1-2m)<0恒成立,求实数m的取值范围.
| a |
| a2-1 |
(1)求f(x)的解析式;
(2)判断f(x)的奇偶性与单调性;
(3)对于f(x),当x∈(-1,1)时,f(1-m)+f(1-2m)<0恒成立,求实数m的取值范围.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)换元法:令t=logax,则x=at,代入函数式可得解析式,利用奇偶函数的定义可判断;
(2)利用函数的奇偶性的定义进行判断,分a>1和0<a<1两种情况进行讨论,利用指数函数的单调性可作出判断;
(3)利用函数的单调性和奇偶性进行求解.
(2)利用函数的奇偶性的定义进行判断,分a>1和0<a<1两种情况进行讨论,利用指数函数的单调性可作出判断;
(3)利用函数的单调性和奇偶性进行求解.
解答:
(本题13分)解:(1)令logax=t则x=at,
∴f(t)=
(at-a-t),
∴f(x)=
(ax-a-t);
(2)∵f(-x)=
(a-x-ax)=-f(x),
∴f(x)为奇函数;
当a>1时,a-x递减,-a-x递增,ax递增,所以ax-a-x递增,
又
>0,所以f(x)在R上递增;
当0<a<1时,a-x递增,-a-x递减,且ax递减,所以ax-a-x递减,
又
<0,故此时f(x)递增;
综上,当a>0且a≠1时,f(x)在R上递增.
(3)f(1-m)+f(1-2m)<0,
∴f(1-m)<-f(1-2m),
∵f(x)为奇函数,且是增函数
∴f(1-m)<(2m-1)
∴
,
解得:
<m<1.
∴f(t)=
| a |
| a2-1 |
∴f(x)=
| a |
| a2-1 |
(2)∵f(-x)=
| a |
| a2-1 |
∴f(x)为奇函数;
当a>1时,a-x递减,-a-x递增,ax递增,所以ax-a-x递增,
又
| a |
| a2-1 |
当0<a<1时,a-x递增,-a-x递减,且ax递减,所以ax-a-x递减,
又
| a |
| a2-1 |
综上,当a>0且a≠1时,f(x)在R上递增.
(3)f(1-m)+f(1-2m)<0,
∴f(1-m)<-f(1-2m),
∵f(x)为奇函数,且是增函数
∴f(1-m)<(2m-1)
∴
|
解得:
| 2 |
| 3 |
点评:本题考查函数奇偶性、单调性的判断,属中档题.

练习册系列答案
相关题目
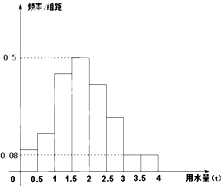 为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图). 如图,在四面体PABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
如图,在四面体PABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.