题目内容
设函数f(x)=|x-2|+|2x+4|.
(1)解不等式f(x)≥6;
(2)若关于x的不等式f(x)≤|2a+1|的解集不是空集,试求实数a的取值范围.
(1)解不等式f(x)≥6;
(2)若关于x的不等式f(x)≤|2a+1|的解集不是空集,试求实数a的取值范围.
考点:绝对值不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)根据绝对值的代数意义,去掉函数f(x)=|x-2|+|2x+4|中的绝对值符号,求解不等式f(x)≥6;
(2)把关于x的不等式f(x)≤|2a+1|的解集不是空集,转化为关于x的不等式f(x)≤|2a+1|的解集非空,求出函数f(x)的最小值,即可求得a的取值范围.
(2)把关于x的不等式f(x)≤|2a+1|的解集不是空集,转化为关于x的不等式f(x)≤|2a+1|的解集非空,求出函数f(x)的最小值,即可求得a的取值范围.
解答:
解:(1)由于函数f(x)=|x-2|+|2x+4|=
,
故由f(x)≥6可得|x-2|+|2x+4|≥6,
故有 ①
; ②
;③
.
解①求得x≤-
;解②求得0≤x<2;解③求得x≥2.
综上可得,不等式的解集为(-∞,-
]∪[0,+∞);
(2)关于x的不等式f(x)≤|2a+1|的解集不是空集,
即|x-2|+|2x+4|≤|2a+1|的解集不是空集.
由(1)可得当x=-2时,函数f(x)取得最小值为4,
即f(x)=|x-2|+|2x+4|≥4,则|2a+1|≥4,
解得:a≥
或a≤-
.
即a的取值范围是:{a|a≥
或a≤-
}.
|
故由f(x)≥6可得|x-2|+|2x+4|≥6,
故有 ①
|
|
|
解①求得x≤-
| 8 |
| 3 |
综上可得,不等式的解集为(-∞,-
| 8 |
| 3 |
(2)关于x的不等式f(x)≤|2a+1|的解集不是空集,
即|x-2|+|2x+4|≤|2a+1|的解集不是空集.
由(1)可得当x=-2时,函数f(x)取得最小值为4,
即f(x)=|x-2|+|2x+4|≥4,则|2a+1|≥4,
解得:a≥
| 3 |
| 2 |
| 5 |
| 2 |
即a的取值范围是:{a|a≥
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查了绝对值的代数意义,去绝对值体现了分类讨论的数学思想;根据分段函数解析式求函数的最值,不等式有解的问题转化为求函数最值问题,属中档题.

练习册系列答案
相关题目
与向量
=(1,-3,2)垂直的一个向量的坐标为( )
| a |
| A、(1,3,2) |
| B、(-1,-3,2) |
| C、(-2,-2,-2) |
| D、(1,-3,-2) |
圆x2+y2-2y-1=0关于直线x-2y-3=0对称的圆方程是( )
A、(x-2)2+(y+3)2=
| ||
| B、(x-2)2+(y+3)2=2 | ||
C、(x+2)2+(y-3)2=
| ||
| D、(x+2)2+(y-3)2=2 |
已知函数f(x)=sin2x+acos2x图象的一条对称轴是x=
,则下列说法中正确的是( )
| π |
| 12 |
A、f(x)的最大值为1-
| ||
B、f(x)在[0,
| ||
C、f(x)在[-
| ||
D、(
|
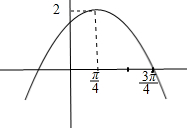 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<