题目内容
在集合M={
,
,1,2,3}的所有非空子集中任取一个集合,恰满足条件“对?∈A,则
∈A”的集合的概率是 .
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:先根据集合的定义求出在所有非空子集中任取一个集合,共有26-1=31种,再找到满足对?∈A,则
∈A”的集合的种数,利用古典概型的概率公式求出概率即可
| 1 |
| x |
解答:
解:M={
,
,1,2,3}的所有非空子集中任取一个集合,共有26-1=31种,
其中满足条件“对?∈A,则
∈A”的有{
,3},{
,2},{1},{1,
,3},{1,
,2},={
,
,2,3},{
,
,1,2,3}共7种,
故恰满足条件“对?∈A,则
∈A”的集合的概率是
故答案为:
| 1 |
| 3 |
| 1 |
| 2 |
其中满足条件“对?∈A,则
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
故恰满足条件“对?∈A,则
| 1 |
| x |
| 7 |
| 31 |
故答案为:
| 7 |
| 31 |
点评:本题考查了根据古典概型的概率公式计算随机事件的概率,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
双曲线
-
=1的离心率是( )
| x2 |
| 2 |
| y2 |
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
已知实数x,y满足不等式组
,则2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、9 |
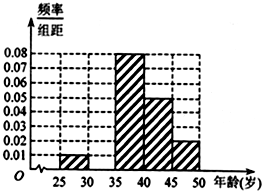 某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )
某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[25,50)岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )| A、37.1岁 |
| B、38.1岁 |
| C、38.7岁 |
| D、43.1岁 |
执行如图的程序框图,若判断框中填入“k>8”,则输出的S=( )


| A、11 | B、20 | C、28 | D、35 |
