题目内容
6.下列命题中真命题的序号为(1).(1)命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0.”
(2)若A>B,则sinA>sinB.
(3)已知数列{an},则“an,an+1,an+2成等比数列”是“$a_{n+1}^2={a_n}{a_{n+2}}$”的充要条件
(4)已知函数$f(x)=lgx+\frac{1}{lgx}$,则函数f(x)的最小值为2.
分析 直接写出全程命题的否定判断(1);举例说明(2)(3)错误;求出函数的值域判断(4).
解答 解:对于(1),命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0”,故(1)是真命题;
对于(2),若A>B,则sinA>sinB,是假命题,如A=390°,B=60°;
对于(3),已知数列{an},由an,an+1,an+2成等比数列成等比数列有$a_{n+1}^2={a_n}{a_{n+2}}$,反之,由$a_{n+1}^2={a_n}{a_{n+2}}$,不一定有an,an+1,an+2成等比数列,
如an=0,an+1=0,an+2=1,∴“an,an+1,an+2成等比数列”是“$a_{n+1}^2={a_n}{a_{n+2}}$”的充分不必要条件,故(3)是假命题;
对于(4),函数$f(x)=lgx+\frac{1}{lgx}$的值域为(-∞,-2]∪[2,+∞),故(4)是假命题.
∴真命题的序号为(1).
故答案为:(1).
点评 本题考查命题的真假判断与应用,考查充分必要条件的判定方法,考查函数值域的求法,是基础题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
17.已知函数 f(x)=kx($\frac{1}{e}$≤x≤e2),与函数$g(x)={(\frac{1}{e})^{\frac{x}{2}}}$,若f(x)与g(x)的图象上分别存在点M,N,使得MN关于直线y=x对称,则实数k的取值范围是( )
| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | (-$\frac{2}{e}$,2e) | D. | [-$\frac{3}{e}$,3e] |
1.给出下列两个命题:
命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.
命题q:若从一只只有3枚一元硬币和2枚五角硬币的储钱罐内随机取出2枚硬币(假设每枚硬币被抽到都是等可能的),则总共取到2圆钱的概率为$\frac{1}{3}$.那么,下列命题中为真命题的是( )
命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为$\frac{π}{4}$.
命题q:若从一只只有3枚一元硬币和2枚五角硬币的储钱罐内随机取出2枚硬币(假设每枚硬币被抽到都是等可能的),则总共取到2圆钱的概率为$\frac{1}{3}$.那么,下列命题中为真命题的是( )
| A. | p∧q | B. | ?p | C. | p∧(?q) | D. | (?p)∧(?q) |
11.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,$f(x)={(\frac{{\sqrt{2}}}{2})^x}-1$,若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0(a>0,a≠1),恰有3个不同的实数根,则实数a的取值范围是( )
| A. | $(\frac{1}{4},1)$ | B. | (1,4) | C. | (4,8) | D. | (8,+∞) |
16.若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是( )
| A. | 在圆上 | B. | 在圆外 | C. | 在圆内 | D. | 不能确定 |
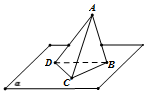 如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.
如图,三棱锥A-BCD的顶点B、C、D在平面α内,CA=AB=BC=CD=DB=4,AD=2$\sqrt{6}$,若将该三棱锥以BC为轴转动,到点A落到平面α内为止,则A、D两点所经过的路程之和是 $2\sqrt{3}π$.