题目内容
17.已知函数 f(x)=kx($\frac{1}{e}$≤x≤e2),与函数$g(x)={(\frac{1}{e})^{\frac{x}{2}}}$,若f(x)与g(x)的图象上分别存在点M,N,使得MN关于直线y=x对称,则实数k的取值范围是( )| A. | [-$\frac{1}{e}$,e] | B. | [-$\frac{2}{e}$,2e] | C. | (-$\frac{2}{e}$,2e) | D. | [-$\frac{3}{e}$,3e] |
分析 求出g(x)的反函数h(x),则g(x)与f(x)的图象在[$\frac{1}{e}$,e2]上有交点,借助函数图象及导数的几何意义即可求出k的范围.
解答 解:g(x)=($\frac{1}{e}$)${\;}^{\frac{x}{2}}$=(e${\;}^{-\frac{1}{2}}$)x关于直线y=x的对称函数为h(x)=log${\;}_{{e}^{-\frac{1}{2}}}$x=-2lnx,
则y=h(x)与y=f(x)=kx在[$\frac{1}{e}$,e2]上有交点,
作出y=h(x)与y=f(x)在[$\frac{1}{e}$,e2]上的函数图象如图所示: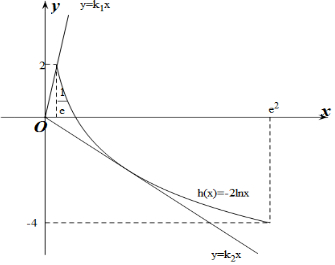
设y=k1x经过点($\frac{1}{e}$,2),则k1=2e,
设y=k2x与h(x)=-2lnx相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{-\frac{2}{{x}_{0}}={k}_{2}}\\{{k}_{2}{x}_{0}=-2ln{x}_{0}}\end{array}\right.$,解得x0=e,k2=-$\frac{2}{e}$.
∴$-\frac{2}{e}$≤k≤2e.
故选B.
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
12.非常数数列{an}是等差数列,且{an}的第5、10、20项成等比数列,则此等比数列的公比为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | 2 | D. | $\frac{1}{2}$ |
9.已知函数f(x)是定义在R上的增函数,若f(a2-a)>f(2a2-4a),则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,3) | C. | (3,+∞) | D. | (-∞,0)∪(3,+∞) |
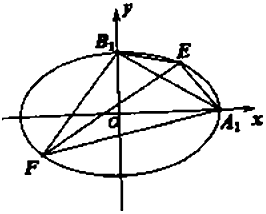 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过 点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过 点A1,B1引椭圆C的两条弦A1E、B1F.